Mapa i plan

Mapa jest podstawowym narzędziem pracy w geografii. Ma szerokie zastosowanie – może pomóc w orientacji w terenie, planowaniu podróży, ale jest też cennym źródłem informacji geograficznych. Dzięki mapom, możliwe jest prowadzenie wielu badań geograficznych.

Spis tematów (kliknij, aby przejść do wyboru tematów)

Wprowadzenie do geografii

V Mapa i plan

1. Pojęcie mapy i planu

Mapa to dwuwymiarowy, graficzny obraz powierzchni Ziemi (lub jej fragmentu, a także innych ciał niebieskich) przedstawiony na płaszczyźnie. Podstawowymi elementami mapy są: skala, legenda, siata kartograficzna (nie zawsze obecna) i treść mapy. Każda mapa wykonana jest z zastosowaniem określonej metody oraz przedstawiona w określonym odwzorowaniu kartograficznym.

Przykładowa mapa przeglądowa – Australia

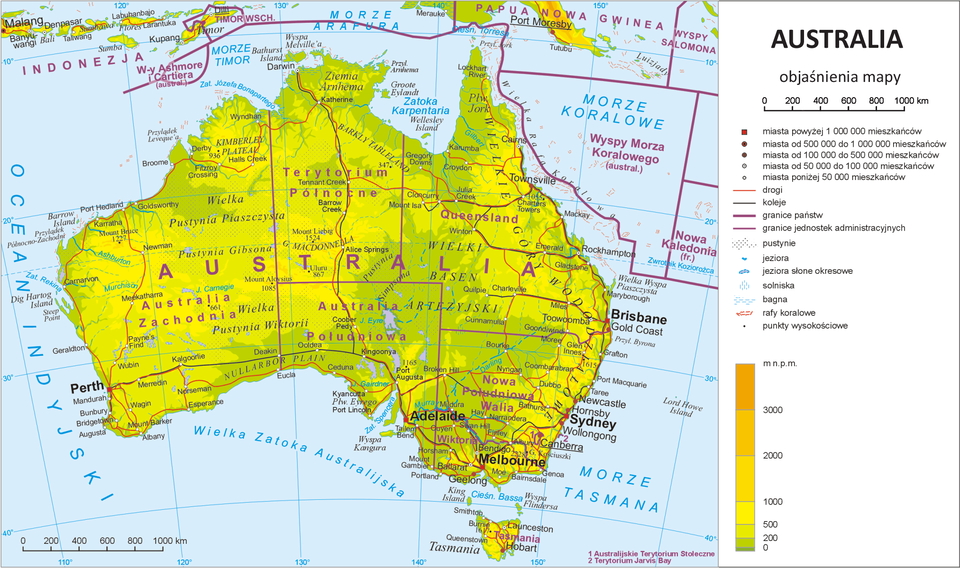
Źródło: http://www.wiking.edu.pl/upload/geografia/images/mapa_przegladowa.jpg

Plan to bardzo szczegółowy obraz niewielkiego fragmentu powierzchni Ziemi, przedstawiony w bardzo dużej skali. Ponieważ na planie przedstawia się niewielkie obszary, możliwe jest pominięcie faktu krzywizny Ziemi (wynikającej z jej kulistości) i związanych z tym deformacji. Dlatego na planie zamiast siatki kartograficznej czasami stosuje się specjalną siatkę kwadratów – mającą na celu pomóc w orientacji w terenie (np. w odnalezieniu punktów spisanych w legendzie), lub zupełnie pomija się ten element.

Przykładowy plan – miasto Lubań

Źródło: http://luban.pl/upload/photos/folders/1010192/plan-lubania.jpg

2. Elementy składowe mapy

1) Siatka kartograficzna, to układ południków i równoleżników na mapie. Ten element jest często pomijany w niektórych mapach tematycznych, ale zasadniczo w mapach ogólnogeograficznych jest to podstawowy element umożliwiający określanie położenia punktów na mapie.

2) Skala mapy – obowiązkowy element każdej mapy i planu, który informuje nas jak bardzo obraz przedstawiony na mapie został pomniejszony w stosunku do rzeczywistości. W rozumieniu matematycznym skala jest ułamkiem zwykłym. W geografii stosujemy 3 rodzaje skali:

• Skala liczbowa – najbardziej popularna. Zapis obejmuje dwukropek z dwiema liczbami po obu jego stronach. W po lewej stronie dwukropka zawsze zapisujemy 1, natomiast po prawej stronie dwukropka – wielkość pomniejszenia. W tym układzie dwukropek zastępuje kreskę ułamkową. W tej skali zarówno lewa jak i prawa strona dwukropka zawsze podane są w centymetrach. Przykładowa skala – 1:10 000.
• Skala mianowana – najłatwiejsza do zrozumienia. Zapis obejmuje dwie liczby, a pomiędzy nimi myślnik. Po lewej stronie zawsze zapisujemy 1 cm, natomiast po prawej stronie myślnika – odpowiadającą mu rzeczywistą odległość w terenie (uproszczoną w najlepszy możliwy sposób). Przykładowa skala – 1 cm – 100 m.
• Podziałka liniowa – graficzna wersja skali, mało popularna – ale jako jedyna nadająca się do map drukowanych, gdzie występuje ryzyko zaburzenia oryginalnych proporcji (skala obrazkowa zmniejsza się lub zwiększa wraz z rysunkiem i zawsze pokazuje prawdziwą skalę mapy). Konstrukcja tej skali opiera się na narysowaniu odcinka i podzielenia go na równe części odpowiadające odległościom. Mierząc linijką odległość między kolejnymi „szczebelkami” podziałki liniowej – wiemy jaka odległość na mapie odpowiada odległości rzeczywistej.

Przykładowe zapisy różnych rodzajów skali z objaśnieniem

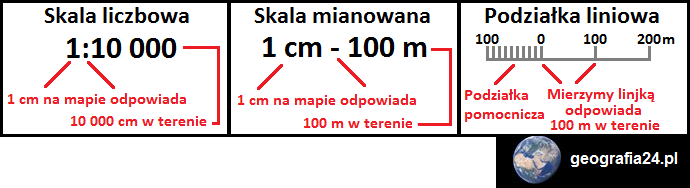
Źródło: Opracowanie własne

Istotnym elementem jest także pojęcie „wielkości” skali. Skale duże to takie, które przedstawiają obraz w dużym przybliżeniu, a więc najbardziej zgodny z rzeczywistością. Z kolei skala mała to taka, która przedstawia obraz w dużym pomniejszeniu. Np. duża skala liczbowa to taka, która ma małą liczbę po dwukropku, a mała – dużą. Tak więc skala 1:100 jest większa od skali 1:1000. Między różnymi rodzajami skali można dowolnie przechodzić, w zależności od celu do jakiej skala ma zostać użyta.

Kolejnym rodzajem skali jest skala polowa. To stosunek powierzchni na mapie do odpowiadającej jej powierzchni w terenie. Stosuje się zapis w postaci skali mianowanej. np. gdy skala liczbowa wynosi 1:10 000 to skala polowa – 1 cm² –  100 000 000 cm² (skalę liczbową podnosimy do kwadratu by uzyskać skalę polową). Taki zapis oznacza, że 1 cm kwadratowy na mapie to 100 000 000 centrymetrów kwadratowych w rzeczywistości. Po uproszczeniu, można tą skalę zapisać jako 1 cm² – 10 000 m² czyli 1 cm² = 1 ha (hektar). W prostszy sposób na skalę polową można zamienić bezpośrednio skalę mianowaną. 1:10 000 to inaczej 1 cm – 100 m. Podnosząc obie strony do kwadratu wiemy, że 1 cm² to 10 000 m².

3) Legenda – obowiązkowy element większości map, choć czasem pomijany gdy na mapie użyto elementy jednoznacznie zrozumiałe. Jest to spis umownych znaków zastosowanych na mapie wraz z ich objaśnieniami. Najczęściej stosuje się znaki zrozumiałe nawet bez czytania ich opisu – dzięki temu legenda ma charakter intuicyjny. Wyróżniamy 3 rodzaje znaków stosowanych w legendzie:

• Znaki punktowe – symbolizują lokalizację obiektów, których powierzchnia i wielkość nie mają większego znaczenia, a najistotniejszy jest sam fakt ich obecności w tym miejscu. Są to pojedyncze obiekty infrastruktury przeróżnego typu, a nawet pojedyncze obiekty przyrodnicze. Najczęściej oznacza się je w sposób intuicyjny, np. parking znakiem drogowym z literą „P”, a kościoły krzyżem.
• Znaki liniowe – symbolizuję położenie obiektów, których powierzchnia nie ma znaczenia, ale istotna jest ich długość i miejsce występowania. Taki rodzaj znaków obejmuje wszelkie drogi, linie energetyczne, linie kolejowe czy cieki (np. rzeki) – przedstawia się w legendzie jako liniowe fragmenty w wybranych kolorach.
• Znaki powierzchniowe – symbolizuję położenie obiektów, które zajmuje duże obszary i ma to istotne znaczenie (oprócz miejsca występowania) w kontekście analizy mapy. Najczęściej odnoszą się do przestrzennie dużych obiektów jak jeziora, lasy, miasta lub ich zabudowa. W legendzie przedstawia się je jako kolorowe prostokąty.

Przykładowa legenda z wyodrębnieniem rodzajów znaków w niej zastosowanych

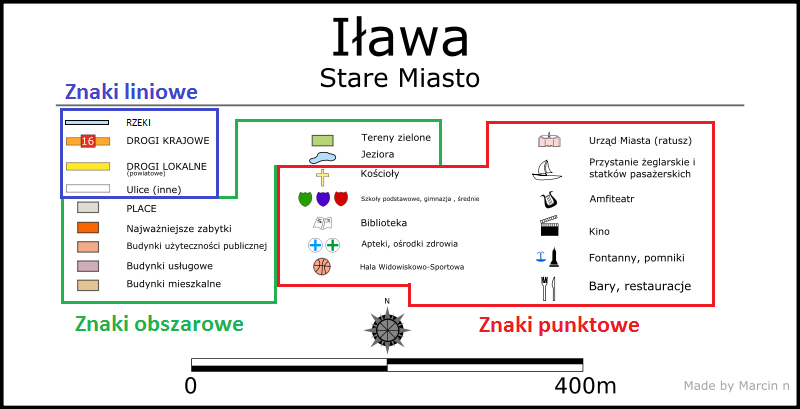
Źródło: https://upload.wikimedia.org/wikipedia/commons/b/b6/Legenda_do_mapy_I%C5%82awy.svg – edytowane

4) Inne elementy – nie muszą pojawić się na mapie

• Kierunek północy – ponieważ wszystkie mapy powinny być zorientowane w kierunku północnym (tzn że przesuwając się w górę mapy poruszamy się na północ), nie jest to element obowiązkowy mapy. Niekiedy jednak możemy spotkać się na mapie ze strzałką lub różą wiatrów obrazującą kierunek północy.
• Tytuł mapy
• Autor mapy
• Rok wykonania mapy
• Oznaczenie godła mapy i nazwa arkusza (mapy topograficzne)

3. Generalizacja kartograficzna

W procesie tworzenia mapy – nanosi się na nią różne elementy istniejące w rzeczywistości. W przypadku planów lub map o dużej skali, możliwe jest dokładne przedstawienie kształtu i wymiaru obiektów oraz dużej liczby różnych szczegółów. Jednak wraz ze zmniejszaniem skali mapy, coraz trudniej jest zachować taki sam poziom szczegółowości, a niekiedy powodowałoby to wręcz nieczytelność mapy. Dlatego im mniejsza skala mapy, tym mniej szczegółowa jest mapa. Proces pomijania mniej istotnych szczegółów oraz upraszczania kształtu obiektów wraz ze zmniejszaniem skali mapy nosi nazwę generalizacji kartograficznej. Generalizacja dzieli się na ilościową (zmniejszenie liczby przedstawionych obiektów) oraz jakościową (upraszczanie kształtu obiektów).

Przykład generalizacji kartograficznej jakościowej (rzeka) i ilościowej (zabudowania)

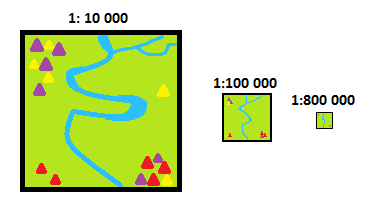
Źródło: Opracowanie własne.

4. Rodzaje map

Istnieje wiele rodzajów map, które tworzy się w odpowiedzi na zapotrzebowanie. Podstawowy podział map obejmuje 3 zasadnicze kategorie – rodzaj treści, wielkość skali oraz przeznaczenie mapy.

1) Podział map ze względu na treść:

• Mapy ogólnogeograficzne – zawiera wszystkie główne elementy powierzchni Ziemi – pokrycie terenu, zabudowa, elementy wodne oraz ukształtowanie powierzchni.
• Mapy tematyczne – przedstawiają tylko wybrane zjawiska ujęte tematem mapy, niemal całkowicie pomijając elementy ogólnogeograficzne – pozostawiając jedynie elementy niezbędne do orientacji w przestrzeni. Niektórzy geografowie przyjmują podział map tematycznych na przyrodniczo-geograficzne i społeczno-gospodarcze.

2) Podział ze względu na skalę:

• Mapy wielkoskalowe – skala nie mniejsza niż 1:200 000 (min. mapy topograficzne i mapy turystyczne).
• Mapy średnioskalowe – skala między 1:200 000 a 1:1 000 000.
• Mapy małoskalowe (zwane też przeglądowymi) – skala mniejsza niż 1:1 000 000.

3) Podział ze względu na przeznaczenie – wiele rodzajów np.:

• turystyczna
• samochodowa
• synpotyczna
• kolejowe
• lotnicze
• morskie
• itp.

5. Odwzorowania kartograficzne

Idealne przeniesienie obrazu powierzchni Ziemi z globusa (3D) na płaską mapę (2D) nie jest możliwe. Podczas tworzenia map dochodzi do zniekształceń. To co pozostaje niezmienne to współrzędne geograficzne – każda mapa, bez względu na przyjęte odwzorowanie, musi zachować prawidłową lokalizację obiektów.

Tak wygląda globus pocięty wzdłuż południków przy przenoszeniu na mapę

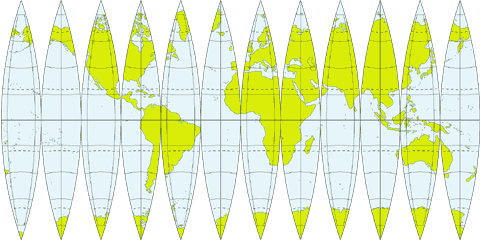
Źródło: http://www.wiking.edu.pl/upload/geografia/images/rozciety_globus.gif

Odwzorowania kartograficzne dzieli się na kilka typów – ze względu na rodzaj zniekształceń, zależne od powierzchni, na którą odwzorowuje się siatkę geograficzną, ze względu na położenie powierzchni odwzorowania oraz inne rodzaje.

1) Odwzorowania według rodzaju zniekształceń

• wiernoodległościowe
• wiernopowierzchniowe
• wiernokątne
• umowne – mają wszystkie zniekształcenia, ale są one niewielkie

Wybrane rodzaje odwzorowań – kropkami pokazano rodzaj zniekształcenia

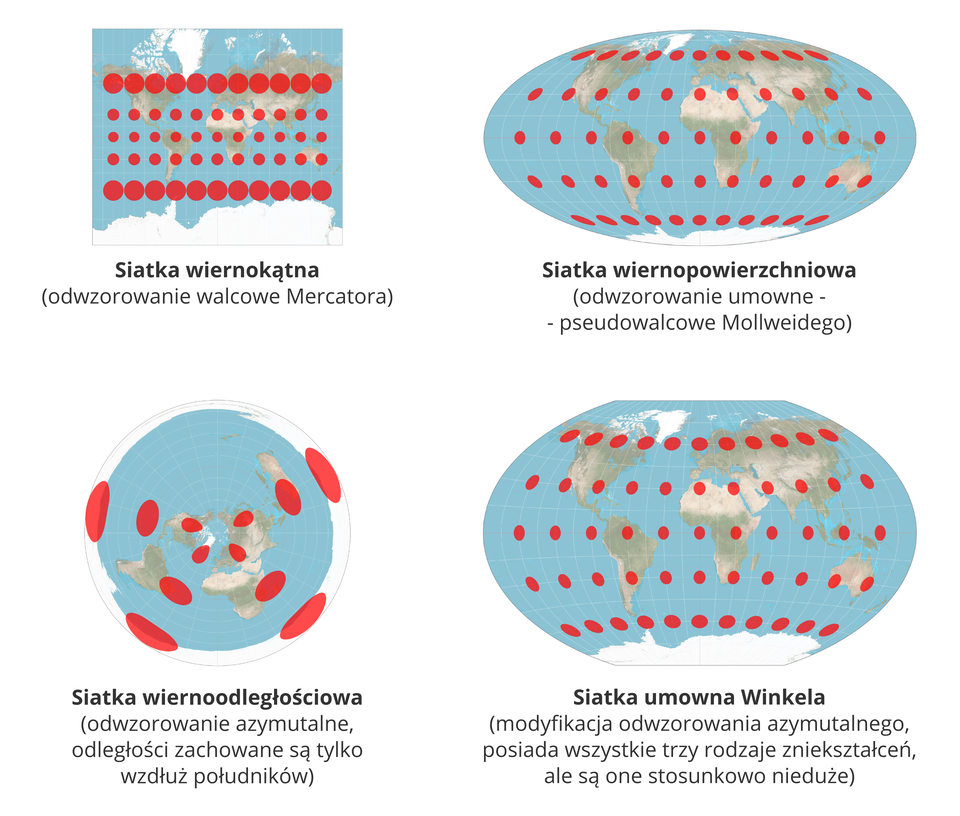
Źródło: https://static.epodreczniki.pl/portal/f/res-minimized/RP869xpG2bwcx/6/960/14Aql4lm1uG0TXNWIsvC3Rkls7oMT3Q8.png, za:Strebe (http://commons.wikimedia.org),Stefan Kühn (http://commons.wikimedia.org),Eric Gaba (http://commons.wikimedia.org), Krzysztof Jaworski, licencja: CC BY-SA 3.0.

2) Odwzorowania według sposobu przyłożenia powierzchni rzutowania

• azymutalne (płaszczyznowe)
• stożkowe
• walcowe
• umowne

Wybrane rodzaje odwzorowań według sposobu przyłożenia rzutowania

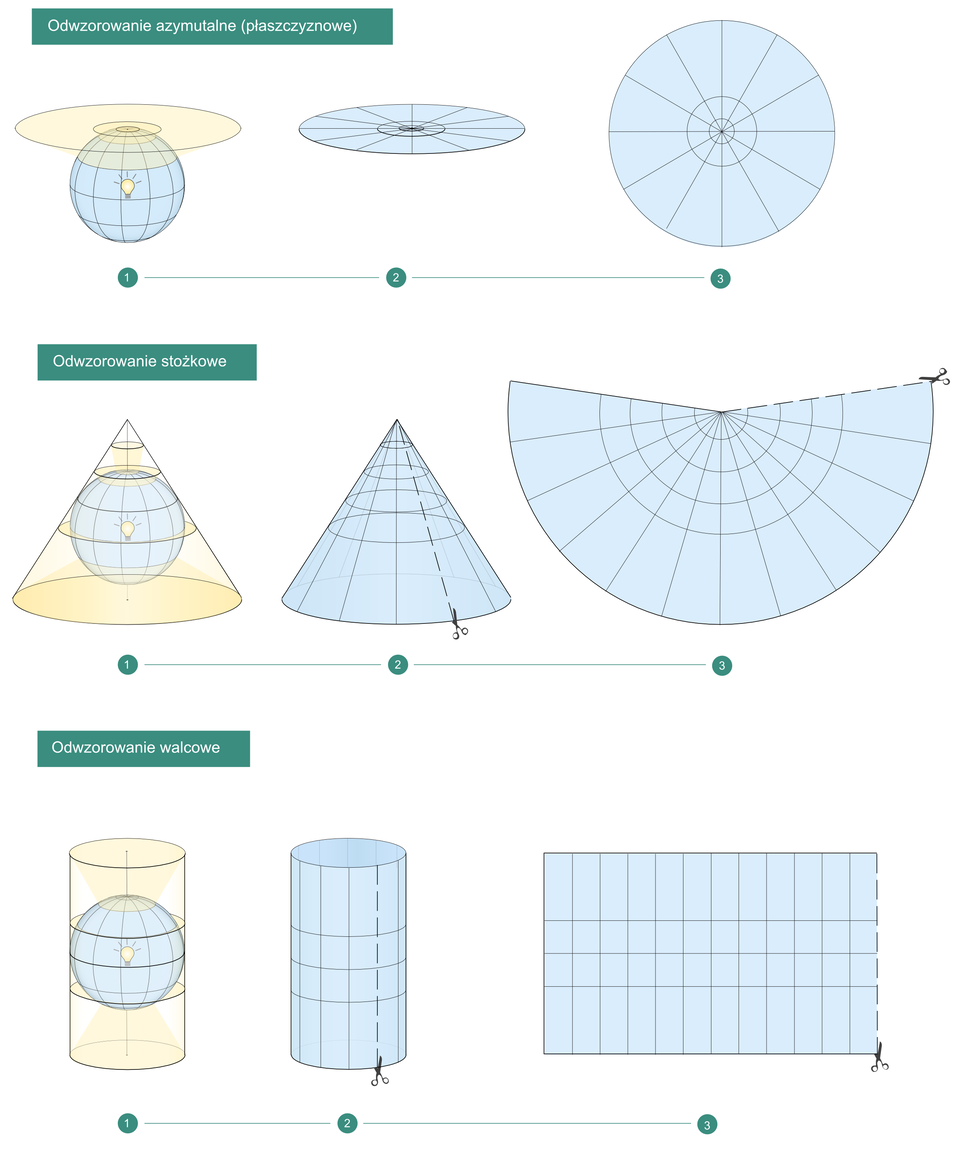
Źródło: https://static.epodreczniki.pl/portal/f/res-minimized/RtIXEpCoNxKa9/7/960/1G94eTlgujr17Wz2ZViw4LaKW4QfwTLC.png za: Olga Mikos, Inductiveload (http://commons.wikimedia.org), licencja: CC BY 3.0.

3) Odwzorowania według położenia powierzchni odwzorowania

• normalne (biegunowe)
• poprzeczne (równikowe)
• ukośne

Wybrane rodzaje odwzorowań według położenia powierzchni odwzorowania

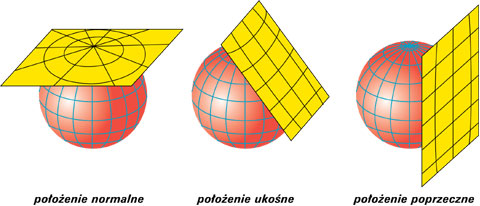
Źródło: http://www.wiking.edu.pl/upload/geografia/images/plaszczyzny_odwzorowania.jpg

4) Najpopularniejsze stosowane odwzorowania

Bez wątpienia najpopularniejszym odwzorowaniem kartograficznym stosowaniem na świecie jest odwzorowanie Merkatora (walcowe równokątne) – zwłaszcza w krajach anglojęzycznych. Kąty są zachowane, a okolice równika są przedstawione bardzo precyzyjnie. Wraz z oddalaniem się od równika w kierunku wysokich szerokości geograficznych – gigantycznym zniekształceniom ulegają powierzchnie i odległości. Ze względu na popularność tego odwzorowania (bardzo podobne odwzorowanie wykorzystuje np. google maps) panuje błędne przekonanie o kolosalnych rozmiarach obszarów polarnych np. Grenlandii i Antarktydy. Np. Grenladnia (rzeczywista powierzchnia niecałe 2,2 mln km²) jest na mapach Merkatora większa od Ameryki Południowej (rzeczywista powierzchnia 17,8 mln km²).

Mapa wykonana z użyciem odwzorowania Merkatora

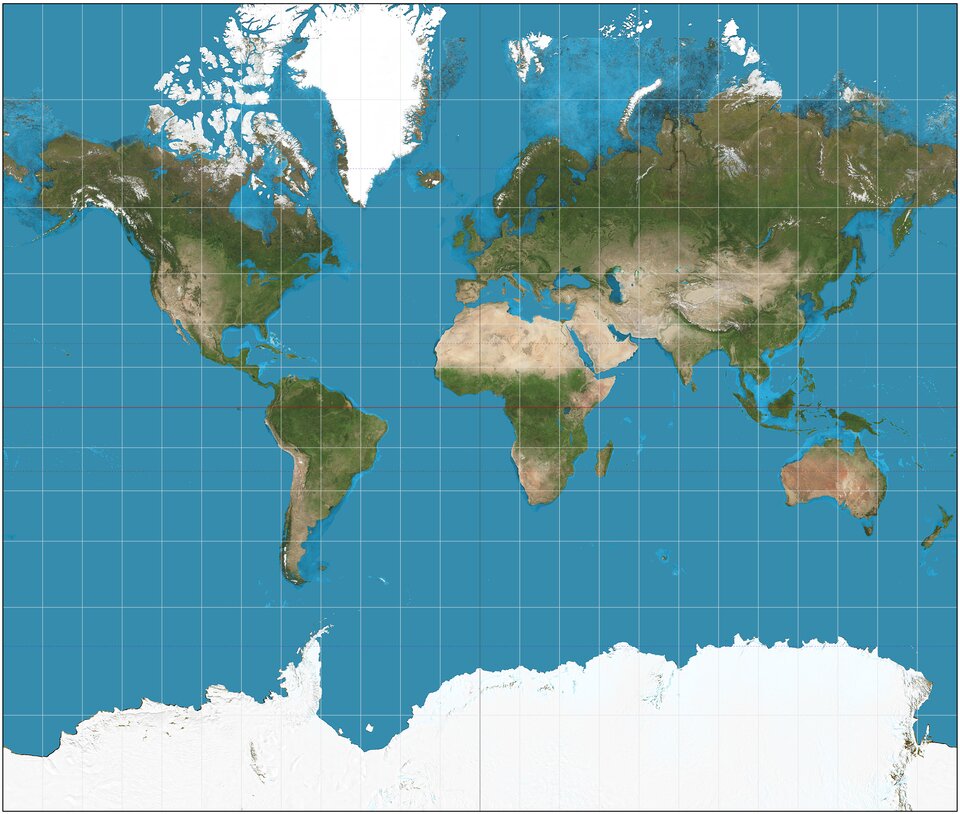
Źródło: https://static.epodreczniki.pl/portal/f/res-minimized/R7Rfh6uC28nW5/11/960/1fzYLaYobx4w6AatCIyTiVrVwteN1tTN.jpg, za:Strebe (http://commons.wikimedia.org), licencja: CC BY-SA 3.0

Powstały nawet ciekawe witryny, zajmujące się pokazaniem rzeczywistych rozmiarów państw – lub jak duże byłyby w odwzorowaniu Merkatora, gdyby leżały w innym miejscu.

Gdyby Polska lezała na Grenlandii to byłaby tak duża, jak na zdjęciu (https://thetruesize.com/)

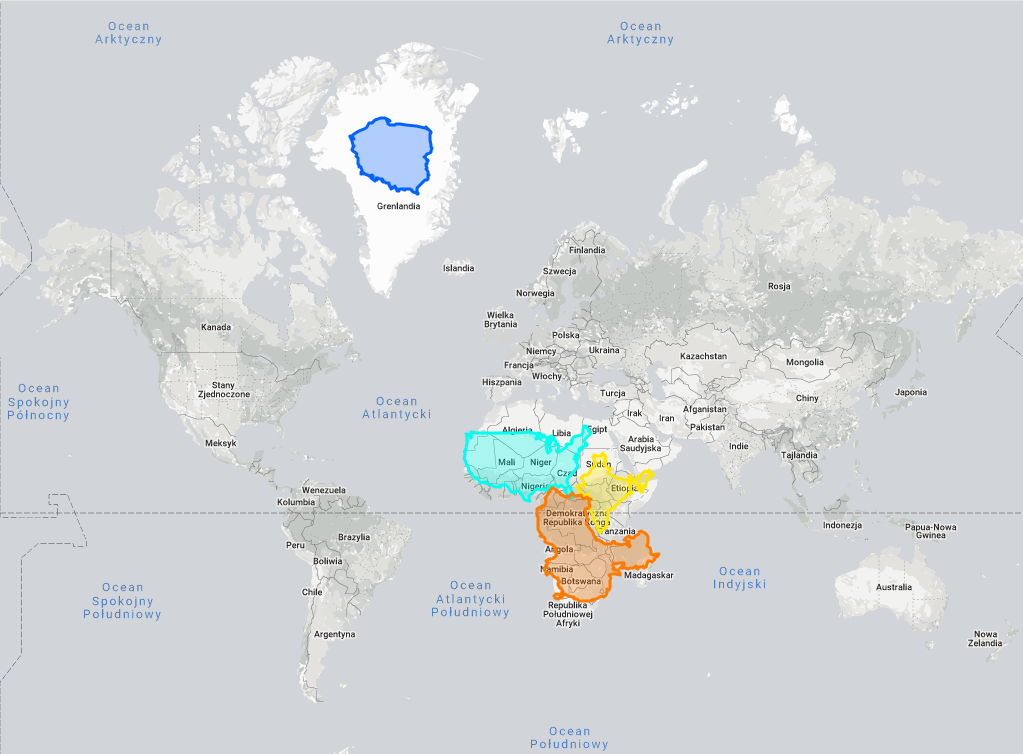
Źródło: https://thetruesize.com/

W Polsce duża popularnością cieszy się odwzorowanie Mollweidego – odwzorowanie pseudowalocwe równopolowe. Duża jego zaletą jest wierne oddanie powierzchni obszarów i mało istotne zniekształcenia pozostałych elementów. Największą słabością są zupełnie błędne kąty w okolicach okołobiegunowych.

Odwzorowanie Mollweidego

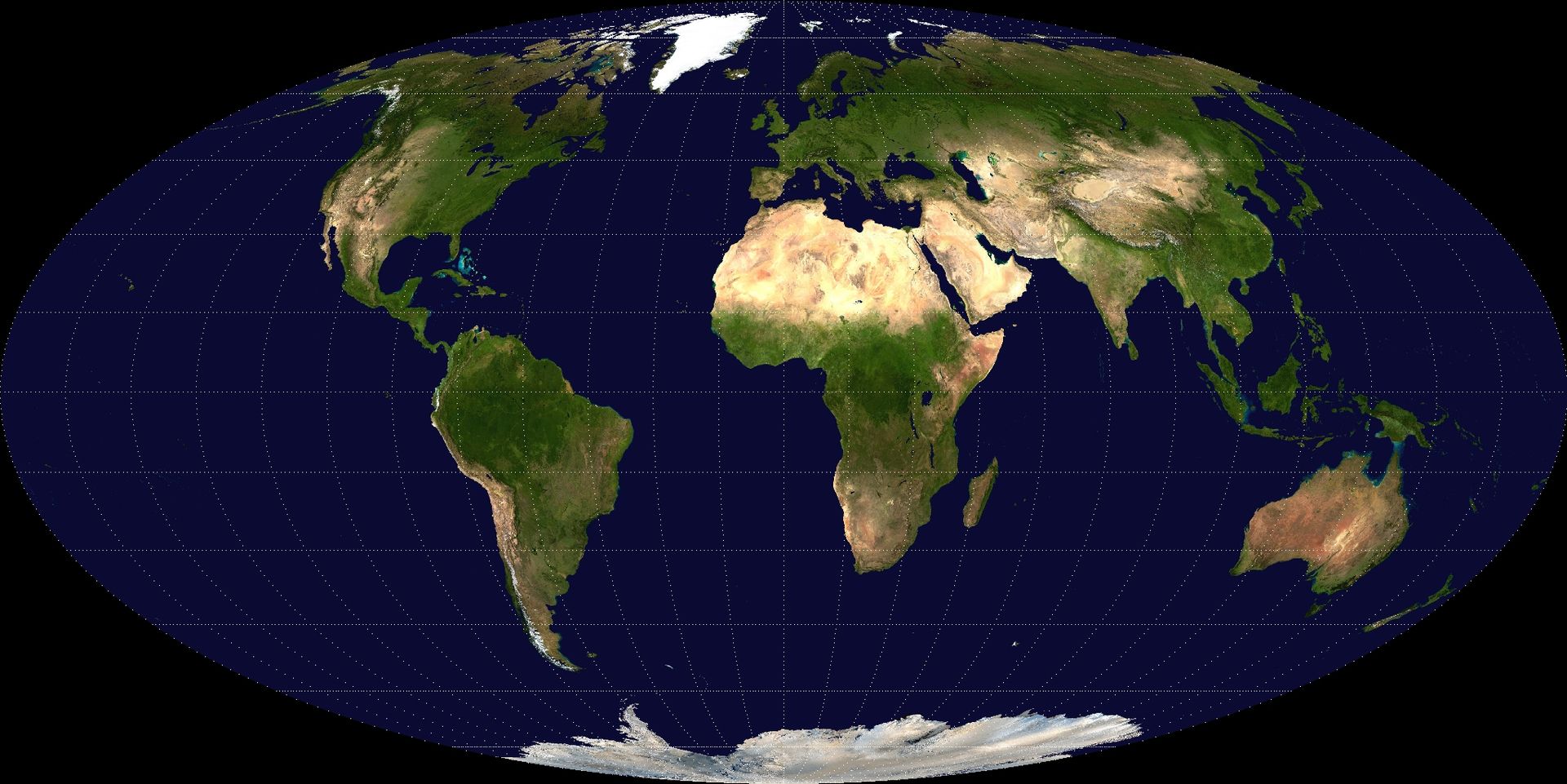
Źródło: https://upload.wikimedia.org/wikipedia/commons/thumb/7/78/Mollweide-projection.jpg/1920px-Mollweide-projection.jpg

6. Przykładowe zadania z mapą i skalą

1) Zadania z przekształcania skali

Zadanie 1 – uzupełnij tabelę dokonując prawidłowego przekształcenia skali liczbowej, mianowanej i podziałki liniowej

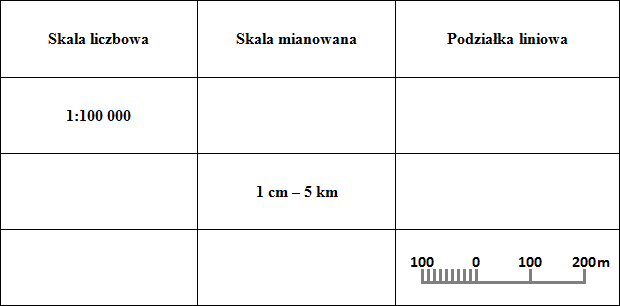
Źródło: Opracowanie własne

Rozwiązanie zadania krok po kroku:

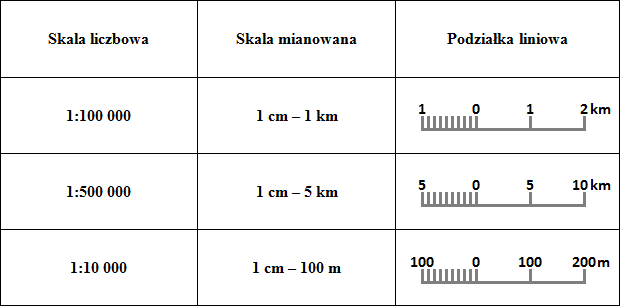
• Skalę liczbową 1:100 000 przekształcamy na skalę mianowaną: 1 cm – 100 000 cm. Teraz skracamy skalę. Wiedząc, że 1 metr = 100 cm, skreślamy dwa zera. W ten sposób uzyskujemy skalę 1 cm – 1 000 m. Wiedząc, że 1 km = 1000 m, dokonujemy kolejnego skrócenia i uzyskujemy finalną skalę 1 cm – 1 km. Możemy też od razu spróbować skreślić 5 zer, jeżeli wiemy że 1 km = 100 000 cm.
• Rysujemy podziałkę liniową identyczną jak ta w ostatniej kolumnie tabeli – z tym, że po każdym „szczebelku” zamiast 100 metrów będzie kolejny 1 kilometr.
• Skalę mianowaną 1 cm – 5 kilometrów zamieniamy najpierw na metry (1 cm – 5 000 metrów), a potem na centymetry (1 cm – 500 000 cm). Teraz zapisujemy skalę w postaci liczbowej – 1:500 000.
• Rysujemy podziałkę liniową z zachowaniem 5 km jako jednostki dla „szczebelka”.
• Podziałkę liniową zamieniamy najpierw na skalę mianowaną. Widzimy, że co każdy „szczebelek” mamy 100 metrów. Należy przyjąć, że autor wykonał szczebelki co 1 cm (można dokonać pomiaru linijką, ale prawdopodobnie uczyni to dalsze wyniki absurdalnymi – załóżmy, że autorowi chodziło o 1 cm – w przypadku map nie wolno nam jednak tak postąpić). W zapisie mianowanym będzie to 1 cm – 100 metrów i tak zapisujemy w polu skali mianowanej.
• Chcąc uzyskać skalę liczbową skalę mianowaną sprowadzamy do centymetrów (1 cm – 100 m => 1 cm – 10 000 cm). Dokonujemy zapisu w postaci liczbowej – 1:10 000.

Więcej zadań ze skalą znajdziesz tutaj (kliknij).

2) Zadania z obliczeń na mapie

Mapa Krety

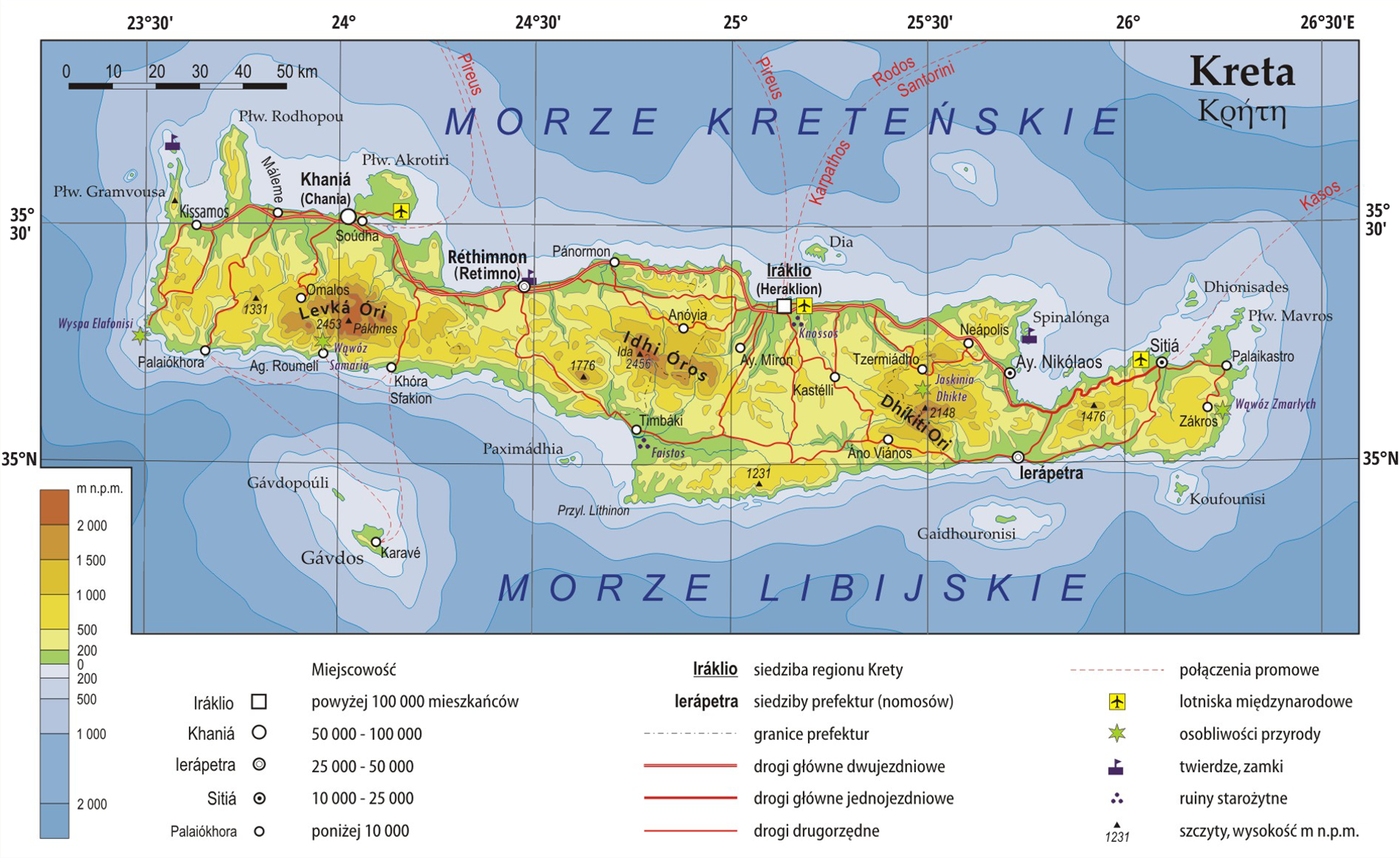
Źródło: https://static.epodreczniki.pl/portal/f/res-minimized/RgE6I9OqU9pkY/7/960/23sEhhH6qqSgvDS0uWMqjc9j4rCsHDGs.png

Zadanie 2 – Korzystając z mapy Krety – oblicz rzeczywistą odległość w linii prostej między Retimno i Heraklion

Rozwiązanie zadania krok po kroku:

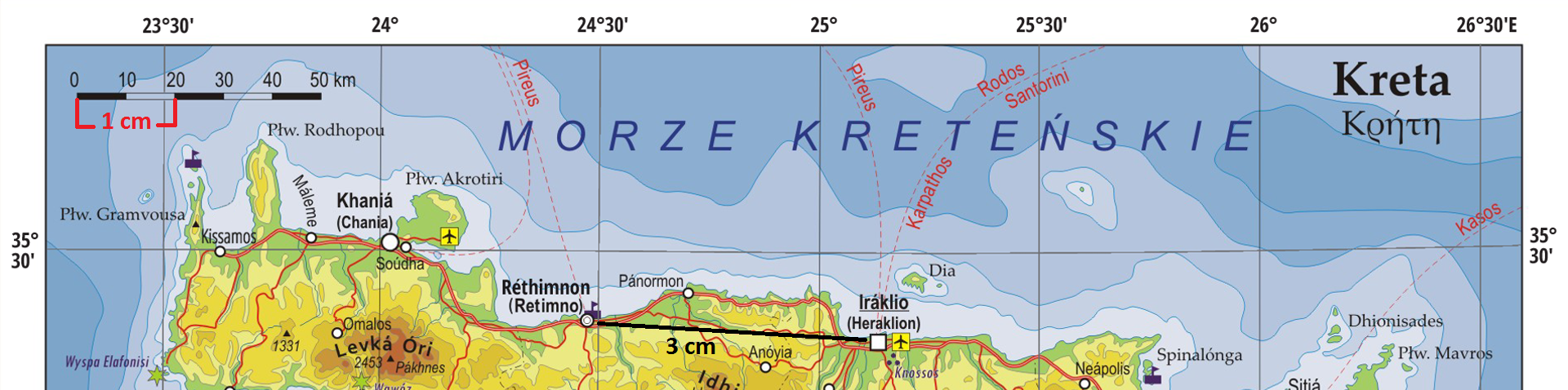
• Na mapie występuje tylko podziałka liniowa. Po zmierzeniu linijką okazuje się, że 1 cm to 2 przejścia w podziałce – czyli 20 kilometrów. Możemy więc zamienić podziałkę liniową na skalę mianowaną: 1 cm – 20 km.
• Odległość w linii prostej między Retimno i Heraklion wynosi niemal dokładnie 3 centymetry.
• Układamy proporcję:

1 cm – 20 km
3 cm – x
x = 3 * 20 km. x = 60 km.

Prawidłowa odpowiedź: Rzeczywista odległość w linii prostej między tymi miejscowościami wynosi 60 kilometrów.

Szybka weryfikacja w google maps utwierdza nas, że uzyskany wynik jest poprawny

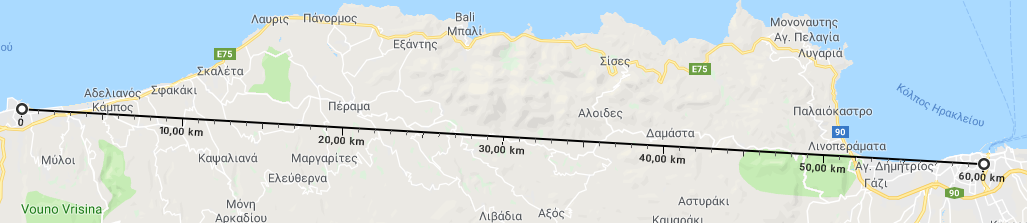
Źródło: https://www.google.pl/maps/@35.3461744,24.771278,11z

Fragment mapy Krety

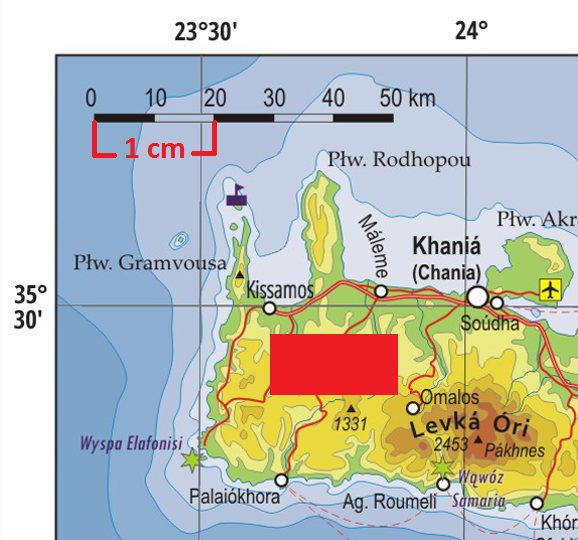
Zadanie 3 – Skorzystaj z fragmentu mapy Krety powyżej. Na mapie zaznaczono obszar planowanych wykopalisk archeologicznych. Oblicz jego powierzchnię w rzeczywistości. Wynik podaj w hektarach. 

Rozwiązanie zadania krok po kroku:

• Wiemy już (z poprzedniego zadania), że 1 cm na mapie odpowiada 20 km w rzeczywistości.
• Aby obliczyć pole czerwonego prostokąt (wzór a*b), musi zmierzyć linijką wymiary obu jego boków. Po zmierzeniu – bok krótszy – 0,4 cm, bok dłuższy – 1,1 cm.
• Pole powierzchni prostokąta to 0,4*1,1 = 0,44 cm².
• Podnosimy skalę do kwadratu – uzyskujemy wynik: 1 cm² – 400 km².
• Tworzymy proporcję:

1 cm² = 400 km²
0,44 cm² = x

• Górną część proporcji mnożymy obustronnie przez 0,44 (400 km²*0,44 = 176 km²)
• Wynik: x = 176 km². Jednak ostateczną powierzchnię obszaru mamy podać w hektarach.
• Wiemy, że 1 km² = 100 ha. 176 *100 ha = 17 600 ha.

Prawidłowa odpowiedź: Rzeczywista powierzchnia czerwonego prostokąta to 17 600 ha.

• Cofając się do etapu dokonania pomiaru długości boków prostokąta to samo zadanie można policzyć drugim sposobem.
• Jeżeli wiemy że 1 cm – 20 km to możemy od razu policzyć rzeczywista długość obu boków.
• Bok krótszy = 0,4 * 20 km = 8 km. Bok dłuższy = 1,1 * 20 km = 22 km.
• Obliczamy powierzchnię prostokąta: 8 km * 22 km = 176 km².
• Następnie zamieniamy na hektary i uzyskujemy identyczny wynik – 17 600 ha.

Fragment mapy Australii

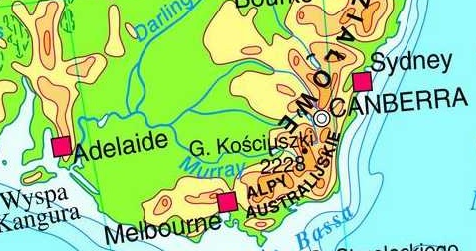
Źródło: http://www.swiatpodrozy.pl/k.php?kid=3&mapID=35#.XL8rf07VK70

Zadanie 4 – Skorzystaj z fragmentu mapy Australii powyżej. Wiedząc, że rzeczywista odległość między Adelaide i Sydney wynosi w linii prostej 160 kilometrów, oblicz skalę mapy. Zapisz skalę w postaci liczbowej.

Rozwiązanie zadania krok po kroku:

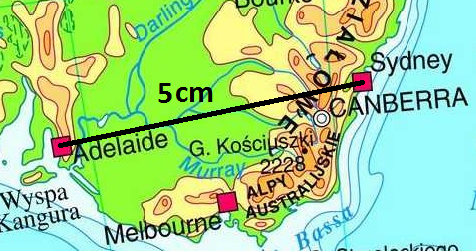
• Mierzymy linijką odległość na mapie między Adelaide i Sydney. Jest to dokładnie 5 centymetrów.
• Wiemy, że odległość na mapie to 5 cm, a odległość rzeczywista to 160 km. Możemy więc ułożyć równanie dla obliczenia skali:

5 cm – 160 km
1 cm – ?

• Dzielimy obustronnie górną część proporcji przez 6. Uzyskujemy wynik: 1 cm – 32 km.
• Uzyskaliśmy już skalę mianowaną, teraz przekształcamy ją na skalę liczbową. 1 cm – 32 km => 1 cm – 32 000 m => 1 cm – 3 200 000 cm. Zapisujemy w postaci liczbowej: 1:3 200 000.

Prawidłowa odpowiedź: Skala liczbowa tej mapy wynosi 1:3 200 000.