Czas na Ziemi

Zarówno ruch obiegowy jak i obrotowy, wyznaczają rytm życia na Ziemi. Obieg Ziemi umożliwia pomiar czasu w latach, z kolei obrót Ziemi – w dniach. Wraz z rozwojem cywilizacyjnym, ludzkość nauczyła się dokonywać coraz dokładniejszych pomiarów czasu.

Spis tematów (kliknij, aby przejść do wyboru tematów)

Wszechświat i Ziemia

V Czas na Ziemi

Pomiar czasu jest jedną z kluczowych umiejętności. Istotny jest przy tym fakt, że w każdym miejscu na Ziemi rzeczywisty czas jest inny, choć wydarzenia mają miejsce w tym samym momencie.

1. Historyczne pomiary jednostek czasu

Pierwotne pomiary czasu, wobec braku odpowiednich umiejętności technicznych, oparte były na obserwacji sił przyrody. Rytm dobowy wyznaczały wschody i zachody Słońca, rytm letni – pory roku. Z czasem wyznaczano także rytm miesięczny – na podstawie faz Księżyca. Dalsze obserwacje astronomiczne umożliwiły z czasem wykształcenie bardziej precyzyjnych jednostek czasu.

Współczesny podział jednostek czasu wywodzi się ze starożytnej Babilonii. To właśnie tam dokonano podziału godziny na 60 minut o jednakowej długości. Następnie dobę podzielono na 24 godziny, wymyślono też 7-dniowy tydzień. Kluczowym osiągnięciem było wymyślenie miesięcy, których ilość ustalono na 12 – co było efektem właśnie obserwacji faz Księżyca (czas ponownego osiągnięcia przez Księżyc tej samej pozycji względem Ziemi – 29,5 dnia).

Istotnym osiągnięciem ludzkości było też opracowanie kalendarza. Zupełnie różne kalendarze powstały w starożytnych cywilizacjach (np. Aztecki miał 18 miesięcy, Egipski – 3 pory roku po 4 miesiące, Babiloński – 12 miesięcy po 29 i 30 dni). Pierwszą uporządkowaną reformę rachuby czasu przeprowadził Rzymski władca – Juliusz Cezar. W 46 r. p.n.e. wprowadził nowy kalendarz – nazwany od jego imienia – Juliańskim. Kalendarz dzielił rok na 365 dni, a co 4 lata  rok miał 366 dni. Miesiące miały tak jak obecnie – 30 lub 31 dni, a luty 28 dni (co 4 lata – 29).

Z czasem jednak zaobserwowano, że z biegiem lat pory roku przesuwają się względem dat kalendarza. Kalendarz Juliański spóźniał się o 1 dzień na każde 128 lat. Dlatego w 1582 r., kiedy podjęto próbę reformy – różnica wynosiła już 12 dni. Na polecenie Papieża Grzegorza XIII wprowadzono kalendarz nazwany gregoriańskim (obowiązuje do dziś). Reforma przesuwała czas natychmiast o 10 dni do przodu (likwidując ówczesne przesunięcie czasu o 10 z 12 dni – przywracając stan faktyczny z 325 r. n.e.) oraz korygowała sposób wyznaczania lat przestępnych – lata o numerach podzielnych przez 100, ale niepodzielne przez 400, nie będą przestępne, przy zachowaniu przestępności pozostałych lat o numerach podzielnych przez 4. Kalendarz gregoriański także cechuj się opóźnieniem, jednak wynosi ono 1 dzień na 3322 lata, co w praktyce oznacza, że póki co nie jest on jeszcze opóźniony, chociaż wprowadzono go prawie 500 lat temu.

2. Czas słoneczny (miejscowy, lokalny)

Czas słoneczny (zwany też czasem miejscowym albo czasem lokalnym), to dokładny, precyzyjny czas określany na podstawie aktualnego górowania Słońca – inny dla każdego punktu na Ziemi, za wyjątkiem wszystkich  punktów leżących dokładnie na tym samym południku (zwanym południkiem miejscowym).

Pierwszych pomiarów czasu Słonecznego dokonywano już w starożytności – wykorzystując w tym celu wbity w ziemię patyk nazywany gnomonem, którego cień rzucany na tarczę wskazywał godzinę słoneczną. Z czasem wynaleziono nieco bardziej skomplikowane zegary słoneczne.

Uliczny zegar słoneczny

Źródło: https://polska-org.pl/foto/3310/Zegar_sloneczny_ul_Nowy_Rynek_Slawa_3310197.jpg

Obecnie nie używa się już prawie zupełnie czasu słonecznego (za wyjątkiem celów teoretycznych), ze względu na wymyślone czasy urzędowe.

Określanie czasu słonecznego to przydatna umiejętność, pozwalająca wyznaczyć rzeczywistą godzinę dowolnego punktu. Obliczenia opierają się czasie ruchu obrotowego Ziemi. Wiedząc, że czas obrotu 360° wynosi 24 godziny (1440 minut), wiemy, że obrót o 15° trwa 1 godzinę (60 minut), a o 1° – 4 minuty.  Z tej zależności wynika identyczna różnica czasu słonecznego – według położenia punktów na określonej długości geograficznej.

Przykładowe zadania:

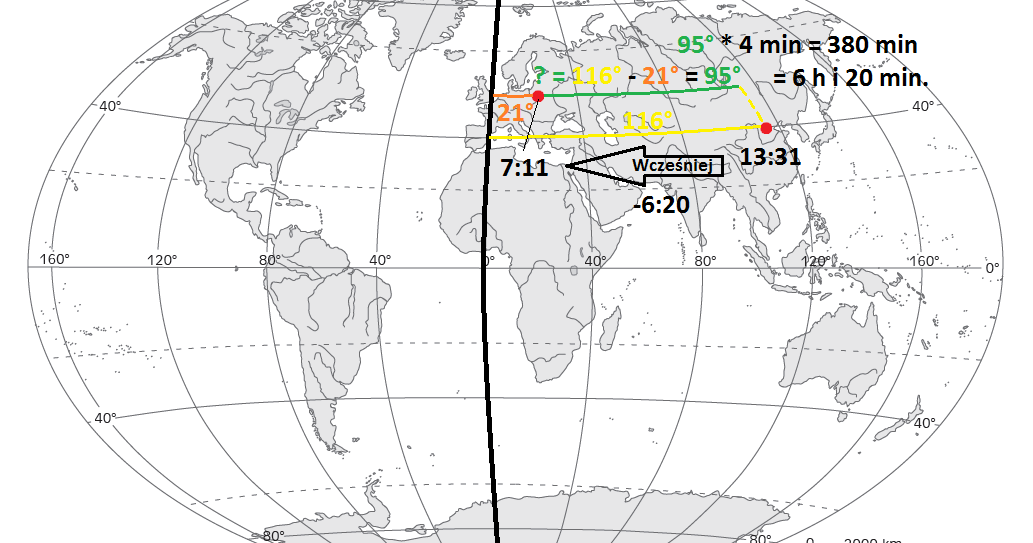
Zadanie 1 – Oblicz godzinę czasu słonecznego w Warszawie (52°N 21°E), wiedząc, że w Pekinie (40°N 116°E) jest godzina 13:31.

Rozwiązanie krok po kroku:

• Pierwszy krok to wybór właściwych współrzędnych. Różnicę czasu oblicza się na podstawie różnicy długości geograficznej – dlatego wybieramy współrzędne 21°E i 116°E.
• Warszawa i Pekin leżą na tej samej półkuli (wschodniej). W tej sytuacji wartości długości geograficznej odejmuje się: 116° – 21° = 95°.
• 1° = 4 minuty. Korzystając z tej prawidłowości obliczamy różnice czasu: 95° * 4 min. = 380 min. = 6 godzin i 20 minut.
• Wiedząc, że w Pekinie jest 13:31 obliczamy godzinę w Warszawie. Warszawa leży na zachód od Pekinu, a więc jest tam godzina wcześniejsza (nie było jeszcze tej godziny, która jest już w Pekinie – gdzie Słońce pojawia się wcześniej): 13:31 – 6:20 = 7:11.

Rysunek pomocniczy (kliknij, aby powiększyć)

Źródło: Opracowanie własne

Odpowiedź: W Warszawie jest godzina 7:11 czasu słonecznego.

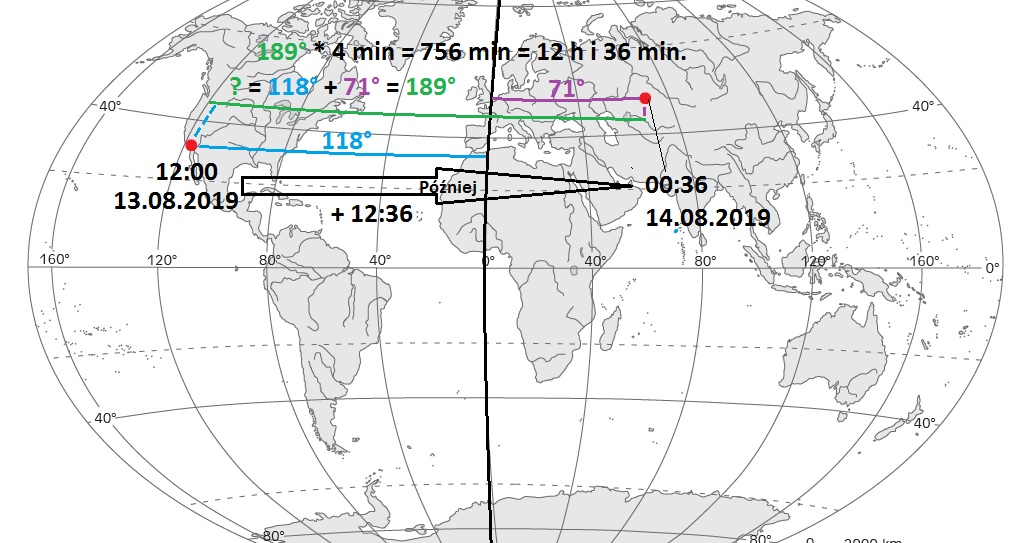
Zadanie 2 – Oblicz datę i czas słoneczny w Nur-Sułtan (51°N 71°E) podczas górowania Słońca w Los Angeles (34°N 118°W) w dniu 13.08.2019 r.

Rozwiązanie krok po kroku:

• Wybieramy współrzędne długości geograficznej – 71°E (Nur-Sułtan) i 118°W (LA).
• Los Angeles i Nur-Sułtan leżą na przeciwnych półkulach. W tej sytuacji wartości długości geograficznej dodaje się: 71° + 118° = 189°.
• 1° = 4 minuty. Korzystając z tej prawidłowości obliczamy różnice czasu: 189° * 4 min. = 756 min. = 12 godzin i 36 minut.
• Wiemy, że Słońce góruje w Los Angeles, co oznacza – że jest tam godzina 12:00 czasu słonecznego. Nur-Sułtan (dawniej Astana) – leży na wschód od Los Angeles, dlatego jest tam godzina późniejsza (innymi słowy południe słoneczne które dopiero jest w LA już dawno temu było w Nur-Sułtan): 12:00 + 12:36 = 00:36.
• Przekroczyliśmy północ przesuwając się na wschód, dlatego należy dodać 1 dzień do kalendarza. Nowa data to 14.08.2019 r.

Rysunek pomocniczy (kliknij, aby powiększyć)

Źródło: Opracowanie własne

Odpowiedź: W Nur-Sułtan jest godzina 00:36 dnia 14.08.2019 r.

Stosując wiedzę z poprzedniego tematu – dotyczącą obliczania górowania Słońca w dniach równonocy i przesileń oraz wiedzę z tego tematu – dotyczącą obliczania godzin słonecznych, można także policzyć współrzędne geograficzne punktu na świecie na podstawie różnicy czasu słonecznego oraz górowania Słońca.

Przykładowe zadanie:

Zadanie 3 – Oblicz współrzędne geograficzne punktu, w którym 22 grudnia obserwator znajduje się w momencie górowania Słońca, wiedząc że górowanie następuje po południowej stronie nieba pod kątem 77°33′, a w tym samym czasie w Londynie jest godzina 9:12.

Rozwiązanie krok po kroku:

• Zadanie należy podzielić na dwa etapy – osobnego określenia szerokości i długości geograficznej.
• Szerokość geograficzną punktu możemy niezwłocznie obliczyć na podstawie górowania Słońca. Kąt jest wysoki, a więc obserwator musi znajdować się gdzieś w okolicy punktu, nad którym Słońce świeci pionowo (Słońce tego dnia świeci pionowo nad zwrotnikiem koziorożca – a więc szukany punkt musi znajdować się w niedalekiej odległości od tego zwrotnika). Wiemy, że Słońce świeci z południa, a więc obserwator musi znajdować się na północ od zwrotnika koziorożca. Ponieważ różnica kąta jest niewielka – 77°33′ (nasz punkt) i 90° (Zwrotnik Koziorożca) – obserwator znajduje się gdzieś w strefie międzyzwrotnikowej (a dokładniej pomiędzy równikiem i zwrotnikiem Koziorożca), ale nadal na półkuli południowej, bo różnica ta jest mniejsza niż 23°26′ (odległość od równika do Zwrotnika Koziorożca). Używamy więc wzoru dla 22 grudnia, strefa międzyzwrotnikowa, półkula południowa:

90° + φ – 23°26′ = 77°33′, gdzie φ to szerokość geograficzna naszego punktu.
φ = 77°33′ + 23°26′ – 90°
φ = 100°59′ – 90°
φ = 10°59′

Już wcześniej ustaliliśmy, że Słońce świeci z południa, ale punkt znajduje się między równikiem i zwrotnikiem, dlatego jego współrzędna to S.

• Szerokość geograficzna naszego punktu to 10°59’S.
• Długość geograficzną punktu obliczamy na podstawie różnicy czasu słonecznego. Wiemy, że nad naszym punktem Słońce góruje, a wiec czas lokalny to 12:00. Z kolei w Londynie (0°) godzina czasu miejscowego to 9:12. Obliczamy różnicę czasu:

12:00 – 9:12 = 2:48 = 2*60 + 48 = 120 +48 = 168 minut.

• Znając różnicę czasu w minutach, możemy obliczyć różnicę odległości kątowej:

1° = 4 min.
?° = 168 min.  -> 42° = 168 min. (bo 168 / 4 = 42).

• Wiemy już, że poszukiwany punkt ma długość geograficzną o 42° inną niż Londyn. Nie wiemy jeszcze czy W czy E. Ponieważ godzina punktu jest późniejsza niż godzina w Londynie, to znaczy, że punkt ten musi znajdować się na wschód od Londynu. Obliczamy współrzędną długości geograficznej poszukiwanego punktu:

0°E + 42° = 42°E.

• Uzyskane współrzędne geograficzne to 10°59’S i 42°E. Punkt ten znajduje się na morzu u wschodnich wybrzeży Mozambiku.

Odpowiedź: Współrzędne poszukiwanego punktu to: 10°59’S 42°00’E.

Zadanie 4 – Oblicz współrzędne geograficzne punktu, w którym 21 marca obserwator znajduje się w momencie górowania Słońca, wiedząc że górowanie następuje po północnej stronie nieba pod kątem 1°11′, a w tym samym czasie w Gdańsku (19°E) jest godzina 13:08.

Rozwiązanie krok po kroku:

• Zadanie wykonujemy analogicznie jak poprzednie.
• Kąt górowania jest skrajnie niski, a więc obserwator na pewno znajduje się na skrajnie dużych szerokościach geograficznych – stosujemy wzory dla strefy umiarkowanej i podbiegunowej. Wiemy, że Słońce góruje po północnej stronie nieba (a tego dnia Słońce góruje na równiku), a wiec obserwator znajduje się na pewno na półkuli południowej. Stosujemy wzór dla 21 marca (taki sam dla całej Ziemi):

90° – φ = 1°11′.
– φ = 1°11′ – 90°
– φ = -88°49′
φ = 88°49′.

• Wiedząc, że obserwator znajduje się na półkuli południowej określamy szerokość geograficzną na 88°49’S.
• Długość geograficzną określamy ponownie na podstawie różnicy czasu słonecznego:

13:08 – 12:00 = 1:08 = 1*60 min + 8 min = 68 min.

• Znając różnicę czasu w minutach, możemy obliczyć różnicę odległości kątowej:

1° = 4 min.
?° = 68 min.  -> 17° = 68 min. (bo 68 / 4 = 17).

• Różnica długości geograficznej między punktami wynosi 17°. Wiemy, że Gdańsk ma długość geograficzną 19°E. Szukany przez nas punkt ma godzinę wcześniejszą niż Gdańsk, a więc musi się znajdować na zachód od Gdańska. Obliczamy długość geograficzną punktu:

19°E – 17° = 2°E.

• Uzyskane współrzędne geograficzne to 88°49’S i 2°E. Punkt ten znajduje się w Antarktyce.

Odpowiedź: Współrzędne poszukiwanego punktu to: 88°49’S 2°00’E.

3. Czas uniwersalny

Aby świat można było podzielić na jakiekolwiek umowne strefy czasu, potrzebny był punkt odniesienia – jakieś miejsce początkowe. Taki czas nazwano czasem uniwersalnym (UTC). Czas uniwersalny oznacza dokładną godzinę czasu słonecznego punktu na południku 0°, za który umownie przyjęto południk przebiegający przez Greenwich w Londynie. 12:00 UTC oznacza więc moment górowania Słońca nad Londynem. Ustalenie czasu UTC umożliwiło podział Ziemi na strefy czasowe – późniejsze i wcześniejsze względem godziny w Londynie.

4. Czas strefowy

Ponieważ posługiwanie się czasem słonecznym jest wybitnie niepraktyczne w codziennym życiu, ustalono że pewne obszary Ziemi można podzielić na strefy o wspólnym czasie – zmieniającym się co godzinę. Z zależności że czas obrotu Ziemi o 15° wynosi 1 godzinę przyjęto, że szerokość każdej strefy czasowej będzie wynosić właśnie 15°. Łącznie na Ziemi wydzielono więc 24 strefy czasowe odpowiadające 24 godzinom. Środek każdej strefy znajduje się o 15° na zachód lub wschód od Londynu. Oznacza to, że granice strefy czasowej godziny 0 wynoszą od 7°30’W do 7°30’E. Polska leży (w większości) w kolejnej strefie – od 7°30’E do 22°30’E – określanej jako strefa +1 (czas środkowoeuropejski). Z kolei wschodnia część Polski leży w strefie +2 (czas wschodnioeuropejski) – od 22°30’E do 37°30’E.

5. Czas urzędowy

Choć podział całej Ziemi na 24 godziny strefowe wydaje się całkiem racjonalny, niestety granice stref czasowych nie pokrywają się z granicami państw. Np. przez Polskę przebiegają dwie strefy czasowe. Są jednak kraje bardzo duże (np. Rosja), przez które przebiega nawet 10 stref czasowych. Z powodów społecznych, wymyślono więc czas urzędowy czyli taki, który obowiązuje na określonym (lub całym) terytorium danego państwa, nawet jeżeli jest to sprzeczne z czasem strefowym. Dlatego w całej Polsce obowiązuje jeden czas (i stąd zmiana czasu na letni i zimowy – od której planujemy odejść). Podobna sytuacja jest min. na Grenlandii – choć wyspa znajduje się w aż 5 strefach czasowych, na niemal całej wyspie obowiązuje jeden czas. Podobnie jest np. w Chinach. Ponadto niektóre kraje, celowo przenoszą się do innej strefy czasowej, niżby to wynikało z ich położenia. Islandia choć znajduje się w samym środku strefy -1, stosuje czas 0 – identyczny jak w Londynie, z kolei Hiszpania znajdująca się w strefie czasu 0, stosuje czas +1.

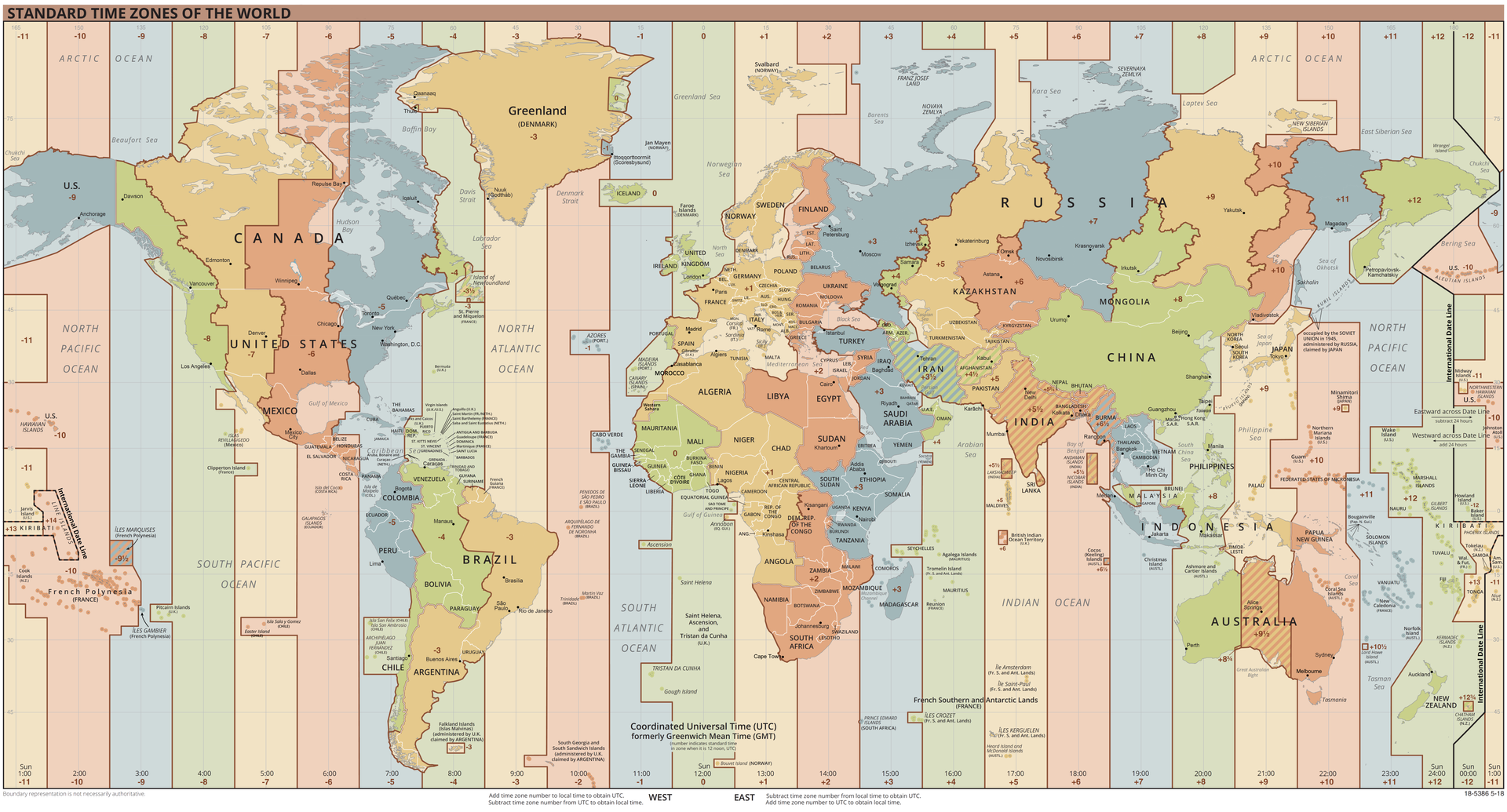
Mapa stref czasowych i czasu urzędowego na Ziemi (zimą) (kliknij aby powiększyć)

Źródło: https://upload.wikimedia.org/wikipedia/commons/thumb/8/88/World_Time_Zones_Map.png/1920px-World_Time_Zones_Map.png

Korzystając z mapy stref czasowych można szybko określić czas (faktycznie występujący) w określonych częściach świata.

Przykładowe zadanie:

Zadanie 1 – Określ godzinę w Nowym Yorku, wiedząc, że w Warszawie jest godzina 16:17.

Rozwiązanie krok po kroku:

• Szukamy na mapie Warszawy i Nowego Yorku. Warszawa znajduje się w strefie czasowej +1, a Nowy York – w strefie -5.
• Obliczamy różnicę czasu strefowego: 1 – (-5) = 6. Czas między Warszawą i Nowym Yorkiem różni się o 6 pełnych godzin.
• Obliczamy godzinę w Nowym Yorku: 16:17 -6:00 = 10:17.

Odpowiedź: W Nowym Yorku jest godzina 10:17.

6. Międzynarodowa linia zmiany daty

Początek określania stref czasowych ustalono na południku 0° przebiegającym przez Londyn. Pozostało jeszcze ustalić, w jaki sposób określić początek nowej doby. Po drugiej stronie Ziemi – przedłużeniem południka 0° jest południk 180°, który w naturalny sposób nadawał się na taką granicę – przebiegał przez prawie niezamieszkały i niemal w całości pozbawiony lądów Ocean Spokojny.

Potrzebą określenia miejsca zmiany daty na Ziemi odkryła już wyprawa Ferdynanda Magellana dookoła świata – która mimo prowadzenia precyzyjnych zapisków czasu, przybyła do punktu wyjścia dzień później niż by to wynikało z prowadzonych obliczeń.

W ten sposób opracowano koncepcję międzynarodowej linii zmiany daty – czyli miejsca, którego przekroczenie będzie oznaczało zmianę dnia w kalendarzu, z zachowaniem godziny wynikającej z czasu słonecznego.

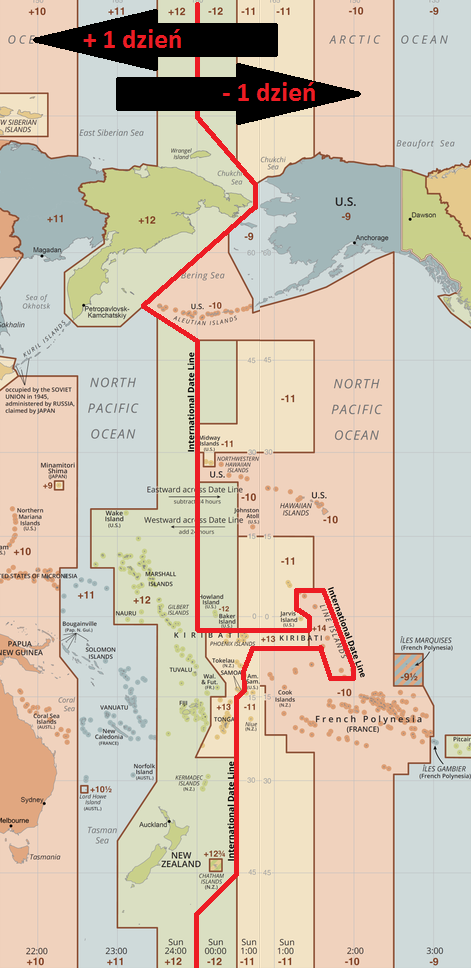
Ostatecznie ustalono przebieg międzynarodowej linii zmiany daty z uwzględnieniem granic państw na Oceanie Spokojnym (a wiec tylko częściowo wzdłuż południka 180°). W ten sposób doszło do bardzo ciekawej sytuacji w której państwo Kiribati posiada (wydającą się całkowicie absurdalną) strefę czasową +14, (chociaż powinna to być strefa -12).

Międzynarodowa Linia Zmiany Daty

Źródło: Opracowanie własne na podstawie: https://upload.wikimedia.org/wikipedia/commons/thumb/8/88/World_Time_Zones_Map.png/1920px-World_Time_Zones_Map.png

Zasada działania Międzynarodowej Linii Zmiany Daty zasadniczo jest dosyć prosta. Przekraczając ją w kierunku zachodnim (w lewo – z półkuli zachodniej na półkulę wschodnią): dodajemy 1 dzień, natomiast przekraczając ją w kierunku wschodnim (w prawo – z półkuli wschodniej na półkulę zachodnią): odejmujemy 1 dzień.

Z udziałem MLZD wymyślono wiele ciekawych zadań geograficznych, które związane są z rzeczywistymi następstwami jej istnienia.

Przykładowe zadanie:

Zadanie 1 – Samolot wystartował z San Francisco (122°W) o godzinie 23:09 dnia 05.06.2019 r. i leciał do Tokio (140°E) przez 10 godzin i 50 minut. Podaj godzinę i datę podczas lądowania w Tokio.

Rozwiązanie krok po kroku:

• Zadanie obejmuje 3 fazy: różnicę czasu słonecznego, czas lotu i Międzynarodową Linię Zmiany Daty (ponieważ samolot leci najkrótszą drogą – a więc przez Linię właśnie)
• Pierwszy krok to obliczenie różnicy czasu słonecznego w momencie, gdy samolot podrywa się z pasa startowego w San Francisco. Można to zrobić na dwa sposoby – albo przez południk 0°, albo przez południk 180°.

Przez południk 0°:

122° + 140° = 262°. 262° * 4 min. = 1048 min = 17 h i 28 min.
Tokio leży na wschód od San Francisco: 23:09 + 17:28 = 16:37 następnego dnia (06.06.2019).

Przez południk 180°:

180° – 122° = 58°.
180° – 140° = 40°.
58° + 40° = 98° (odległość kątowa miedzy miastami San Francisco i Tokio).
98° * 4 min = 392 min = 6 h i 32 min.
Tokio leży na zachód od San Francisco – odejmujemy czas: 23:09 – 6:32 = 16:37.
Przekroczyliśmy Międzynarodową Linię Zmiany Daty obliczając różnicę czasu – dodajemy 1 dzień. Nowa data: 06.06.2019 r.

• Wynik jest identyczny, pod warunkiem prawidłowego obliczenia. W momencie startu samolotu z San Francisco w Tokio jest 16:37 dnia 06.06.2019 r.
• Drugi krok to uwzględnienie czasu lotu samolotu. Godzina w Tokio: 16:37 + 10:50 (czas lotu) = 03:27. Przekroczyliśmy północ więc trzeba dodać kolejną dobę: 07.06.2019 r.
• Finalny wynik: 03:27 dnia 07.06.2019 r.
• Nie dodajemy kolejnej doby z Międzynarodowej Linii Zmiany Daty, ponieważ – w pierwszym obliczeniu (przez południk 0°) ją ominęliśmy, a w drugim – przez południk 180° ją dodaliśmy obliczając czas słoneczny – nie dodajemy jej więc po raz drugi.
• Zadanie można także wykonać w innej kolejności:

Start: 23:09 (05.06.2019) + 10:50 (lot) = 9:59 (06.06.2019) + przekroczenie Międzynarodowej Linii Zmiany Daty (+1d) = 9:59 07.06.2019 + różnica czasu słonecznego – przez południk 180°: 6:32 -> 9:59 – 6:32 (bo Tokio jest na zachód od San Francisco) = 03:27 dnia 07.06.2019 r.

Odpowiedź: W momencie lądowania w Tokio będzie 03:27 dnia 07.06.2019 r.