Skala

Skala jest ważnym elementem prezentacji zjawisk w przestrzeni. Służy pomniejszeniu obiektów, w tym zwłaszcza powierzchni. Dzięki skali możemy dowiedzieć się, jak bardzo pomniejszony (lub powiększony) został obiekt oraz obliczyć odległości między punktami.

Skala mapy

1. Rodzaje skali

Wyróżniamy 3 rodzaje skali:

• liczbowa np: 1:300 000

Jest to zapis skali w którym po lewej stronie dwukropka mamy zawsze 1 centymetr na mapie, a po prawej stronie odległość rzeczywistą odpowiadającą 1 centymetrowi na mapie, również wyrażoną w centymetrach. Inną formą zapisu tej skali jest po prostu ułamek zwykły, np. .

• mianowana np: 1 cm – 20 km

Taki zapis skali jest najbardziej czytelny dla odbiorcy. Po lewej stronie myślnika, podobnie jak w skali liczbowej znajduje się 1 centymetr na mapie, a po prawej stronie myślnika odpowiadająca mu odległość rzeczywista, tym razem w dowolnej jednostce.

• podziałka liniowa:

Graficzne przedstawienie skali wykonane jest według zasady, iż odstęp między kolejnymi wartościami zawsze standardowo 1 cm (choć czasem wartość ta może być inna) a nad kolejnymi centymetrami znajdują się odpowiadające im wartości.

2. Przekształcanie skali

W praktyce możliwe jest przekształcanie różnych typów skali na inne, w celu np. zmiany zastosowania. W tabeli poniżej podano przykłady przekształcenia skal:

Słowny zapis skali	Skala liczbowa	Skala mianowana	Podziałka liniowa
1 cm na mapie to 2 metry w terenie	1:200	1 cm – 2 m
1 cm na mapie to 100 metrów w terenie	1: 10 000	1 cm – 100 m
1 cm na mapie to 25 kilometrów w terenie	1:2 500 000	1 cm – 25 km

3. Zastosowanie skali

• Skala liczbowa jest najczęściej stosowaną i najbardziej znaną skalą. Może być zastosowana we wszystkich rodzajach map. Jej największą zaletą jest, iż pozostaje ona niezależna od zastosowanego odwzorowania, które czasem może zniekształcać podziałkę liniową.
• Skala mianowana stosowana jest zdecydowanie rzadziej. Można ją spotkać w rysunku architektoniczno-budowlanym oraz czasami na mapach. Główną zaletą tej skali jest jej najlepsze zrozumienie przez każdą osobę.
• Podziałka liniowa jest obowiązkowym elementem każdej mapy drukowanej, zwłaszcza dotyczącej fragmentów powierzchni Ziemi. Ponieważ w wyniku przekształcenia wielkości na różnych formach wydruku – obraz ulega zmniejszeniu bądź zwiększeniu, pozostałe skale stają się nieprawdziwe. Jedynie podziałka liniowa zachowuje rzeczywistą informację o skali, gdyż odstępy między kolejnymi wartościami zmniejszają się bądź zwiększają wraz z drukowanym obrazem.

4. Zadania ze skalą

Typowo spotykanymi zadaniami szkolnymi ze skalą są: zadania z przekształcenia skali (patrz tabelka wyżej) oraz zadania polegające na obliczeniu odległości rzeczywistej między punktami przy znajomości odległości na mapie, obliczeniu odległości na mapie przy znajomości odległości rzeczywistej oraz obliczenia samej skali przy znajomości obu tych odległości. Poniżej przykłady takich zadań wraz z przykładowymi rozwiązaniami:

Znając już zasady posługiwania się każdą z danych skal, musimy pamiętać o najważniejszej rzeczy – zamianie jednostek. Bez znajomości poprawnej zamiany, nie jesteśmy w stanie wykonać zadań ze skali.

Zadanie 1

Oblicz rzeczywistą odległość miedzy dwoma miastami, jeśli na mapie wynosi ona 10 cm*, a mapę tą wykonano w skali 1:200 000.

1) Używając skali liczbowej, ustalamy odległość rzeczywistą odpowiadającą 1 cm na mapie. 1 cm – 200 000 cm = 2000 m = 2 km

2) Teraz możemy obliczyć odległość rzeczywistą używając proporcji
1 cm – 2 km
10 cm – x km
x = (10*2)/1
x = 20 km

Odp: Rzeczywista odległość między miastami wynosi 20 km.

*Czasami zamiast podanej odległości między miejscowościami/obiektami jest tylko mapa. W takiej sytuacji należy zrobić to samo, co w zadaniu 3 i zmierzyć tą odległość linijką.

Zadanie 2 

Odległość między dwoma punktami w terenie wynosi 450 km. Oblicz ile wynosi ona na mapie w skali 1:900 000.

1) Zamieniamy skale liniową na mianowaną.
1 cm – 900 000 cm = 9000 m = 9 km

2) Teraz układamy proporcję.
1 cm – 9 km
x cm – 450 km
x = (450*1)/9
x = 50 cm

Odp: Odległość na mapie wynosi 50 cm.

Zadanie 3 

Mapa do zadania 3:

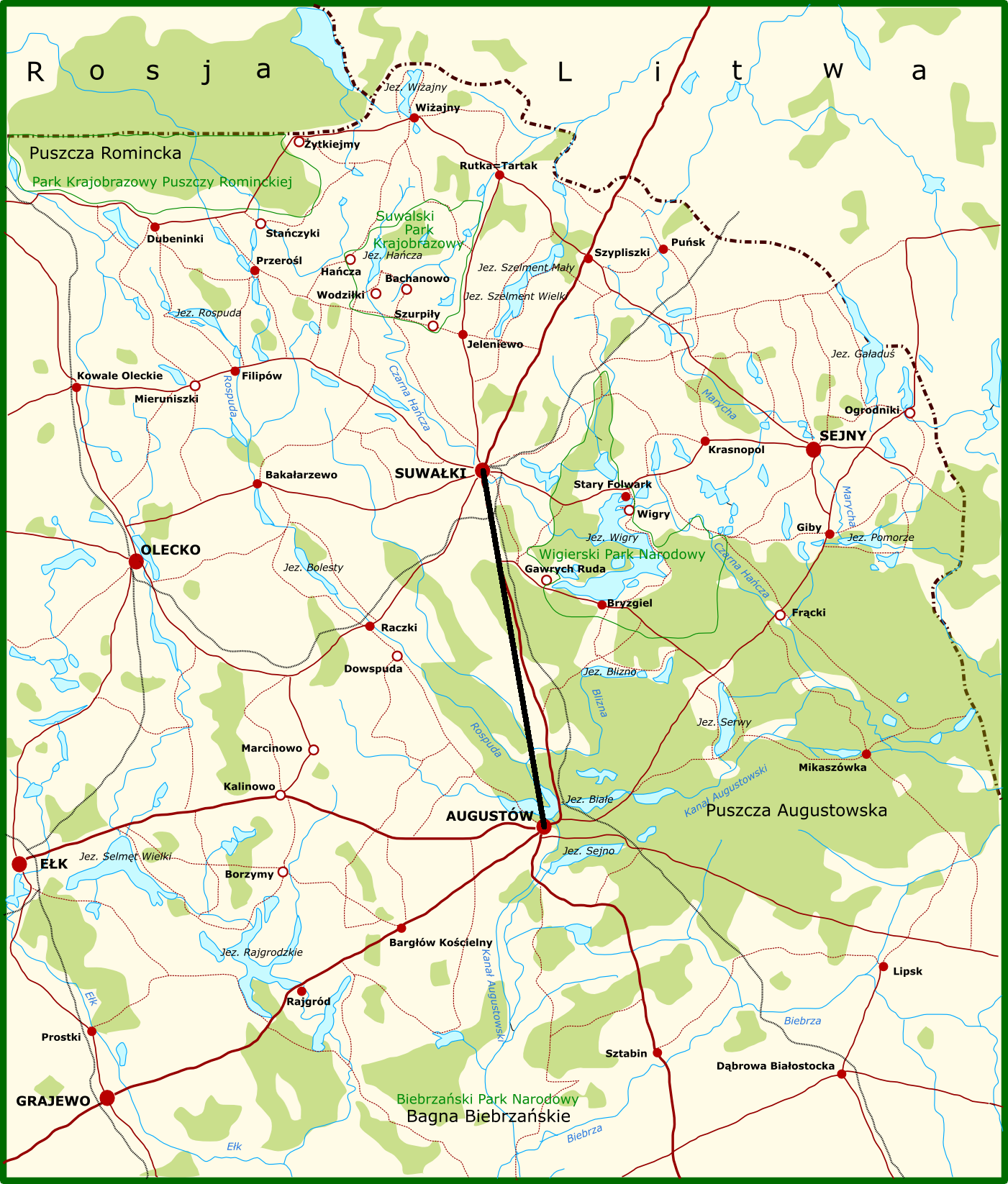
Źródło: Wulfstan; https://upload.wikimedia.org/wikipedia/commons/thumb/2/22/Suwalszczyzna.png/510px-Suwalszczyzna.png

Oblicz w jakiej skali została wykonana mapa powyżej, jeżeli odległość rzeczywista między Suwałkami i Augustowem wynosi 30 km.

1) Mierzymy linijką odległość między miastami w linii prostej, aby poznać odległość między tymi miastami na mapie.

2) Po zmierzeniu okazuje się, że odległość między Augustowem i Suwałkami wynosi 5 cm.
Teraz wiemy, że 5 cm na mapie odpowiada 30 km w terenie.

Za pomocą proporcji obliczamy ile wynosi skala mapy.
5 cm – 30 km
1 cm – x km
x = (30*1)/5
x = 6 km
1 cm – 6 km

3) Zamieniamy skalę mianowaną na liczbową
1 cm – 6 km = 6000 m = 600 000 cm zatem skala liczbowa wynosi 1:600 000

Odp: Mapa została wykonana w skali 1:600 000.

Autor: Bartłomiej Kulas, Agata Wyszkowska

Sprawdzono pod względem merytorycznym: mgr Bartłomiej Kulas