Współrzędne w geografii odgrywają kluczową rolę – służą do realizacji podstawowego zadania geografii – określania położenia różnych obiektów na Ziemi. Do ich wyznaczania stosuje się układ współrzędnych oparty o szerokość i długość geograficzną – jest on w pewnym stopniu podobny do układu współrzędnych opartego o oś X i Y wykorzystywanego w matematyce.
Spis tematów (kliknij, aby przejść do wyboru tematów)
Współrzędne w geografii
I Szerokość i długość geograficzna
Geografia jest nauką o przestrzeni. Jej podstawowym zadaniem jest określanie gdzie znajdują się różne punkty i obiekty. Graficznym obrazem realizacji tej misji geografii są tworzone mapy i globusy. Nanosi się na nie specjalny układ współrzędnych, który umożliwia matematyczne określenie położenia każdego obiektu.
1. Układ równoleżników i południków – siatka geograficzna
Aby możliwe było określenie lokalizacji punktu, konieczne jest wyznaczenie punktów odniesienia względem których można obliczyć odległość. W matematyce stosuje się w tym celu układ współrzędnych oparty o poziomą oś X i pionową oś Y. Podobnie jest w geografii – aby możliwe było określenie położenia np. Warszawy stworzono specjalną siatkę, zwaną siatką geograficzną, na którą składają się południki i równoleżniki. Istnienie południków i równoleżników akurat w tym miejscu, w którym zostaną narysowane ma całkowicie “umowny” charakter, tzn. linie te nie istnieją w rzeczywistości, ale cały Świat przyjął ich określoną lokalizację, dla ujednolicenia wspólnej wiedzy geograficznej.
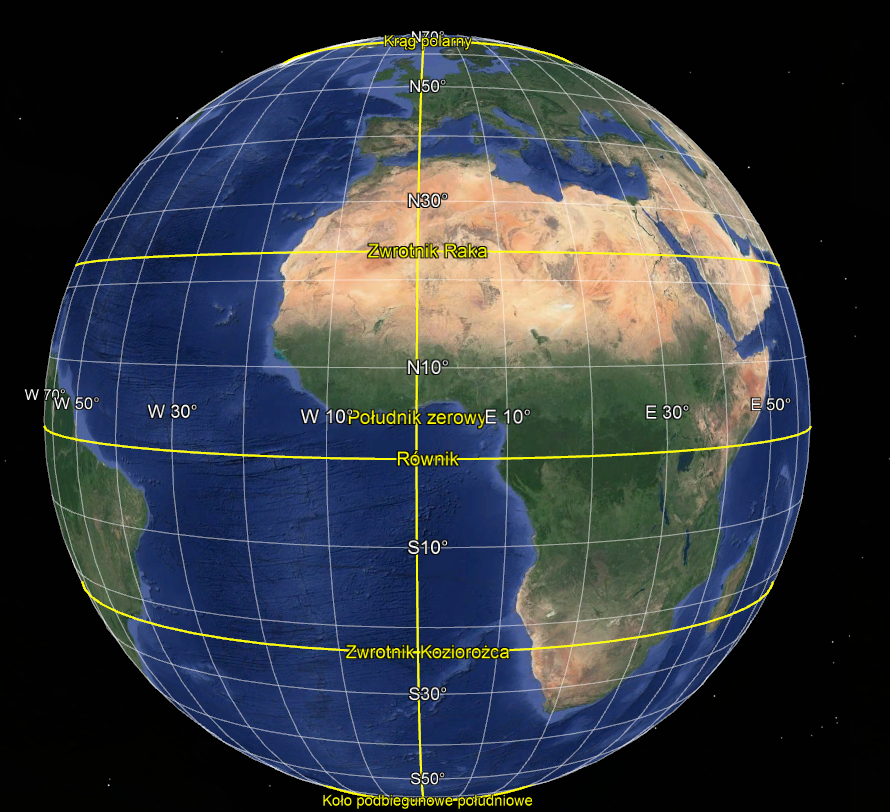
Siatka geograficzna – pełny układ południków i równoleżników na modelu Ziemi w Google Earth
Źródło: Google Earth.
Cała siatka geograficzna dzieli się na dwa podstawowe elementy składowe – biegnące “w poziomie” – równoleżniki oraz mające układ “pionowy” – południki.
Równoleżnik – to okrąg obiegający Ziemię dookoła. Najdłuższym równoleżnikiem jest równik ~40 075 km – jest on także nazywany równoleżnikiem początkowym. Został wyznaczony tam, gdzie okrąg wokół Ziemi jest najdłuższy, a Ziemia – “najszersza”. Kolejne równoleżniki są do równika równoległe (stąd ich nazwa) i są tym krótsze im bliżej są biegunów. Na biegunie północnym i południowym równoleżniki są punktami i mają długość 0 km (zero). Choć istnieje nieskończenie wiele równoleżników, oprócz równika istnieją jeszcze 4 szczególnie ważne równoleżniki: dwa zwrotniki: raka (23°26’N) i koziorożca (23°26’S) oraz dwa koła podbiegunowe (północne – 66°34’N i południowe – 66°34’S). Ich położenie akurat w tym miejscu wynika z nachylenia osi obrotu Ziemi. Technicznie równoleżnikami są także bieguny, chociaż faktycznie są one punktami o współrzędnych odpowiednio: 90°N – biegun północny oraz 90°S – biegun południowy. Równik stanowi podstawę do podziału Ziemi na dwie półkule – północną i południową.
Południk – to półokrąg (linia) łącząca ze sobą biegun północny i biegun południowy (najkrótszą możliwą drogą). Nazwa nawiązuje do linii biegnącej z północy na południe. Długość każdego południka to około 20 000 km. Wśród nieskończonej liczby umownych południków, istnieją dwa szczególne południki o precyzyjnie określonym położeniu – południk początkowy zwany południkiem zerowym (0°) oraz południk 180° – dokładnie po drugiej stronie Ziemi od południka zerowego. Południk zerowy znajduje się w dzielnicy Londynu – Greenwhich (obecnie – od 1984 r. około 100 metrów od pierwotnie ustalonej lokalizacji), dlatego często bywa też nazywany południkiem Greenwhich. Jego wyznaczenie było wynikiem decyzji politycznej, z kolei południk 180° jest po prostu jego przedłużeniem po drugiej stronie planety. Południk zero stanowi podstawę do podziału Ziemi na dwie półkule – wschodnią oraz zachodnią.
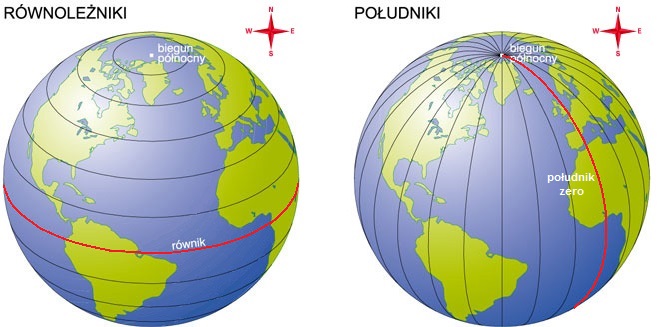
Układ wybranych równoleżników i południków – na tle równika i południka zero
Źródło: http://www.wiking.edu.pl/article.php?id=949
Cechy równoleżników i południków – podobieństwa i różnice – dla zaawansowanych
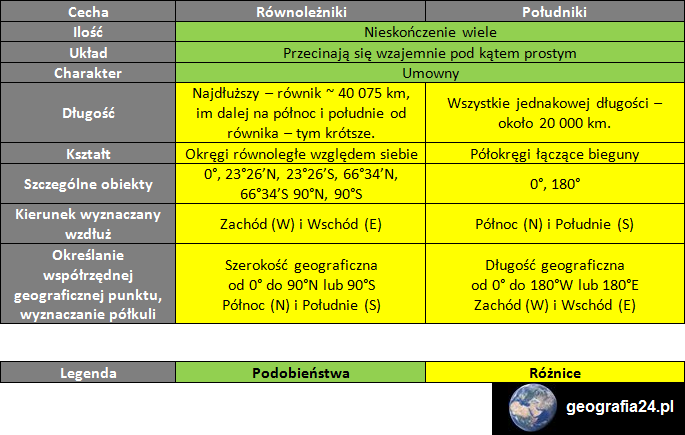
Źródło: Opracowanie własne.
2. Kierunki Świata
Istnienie na Ziemi równoleżników i południków pozwala dokonać podziału Ziemi na półkule. Każdy z podziałów tworzy dwie półkule, co łącznie daje nam cztery podstawowe części Ziemi.
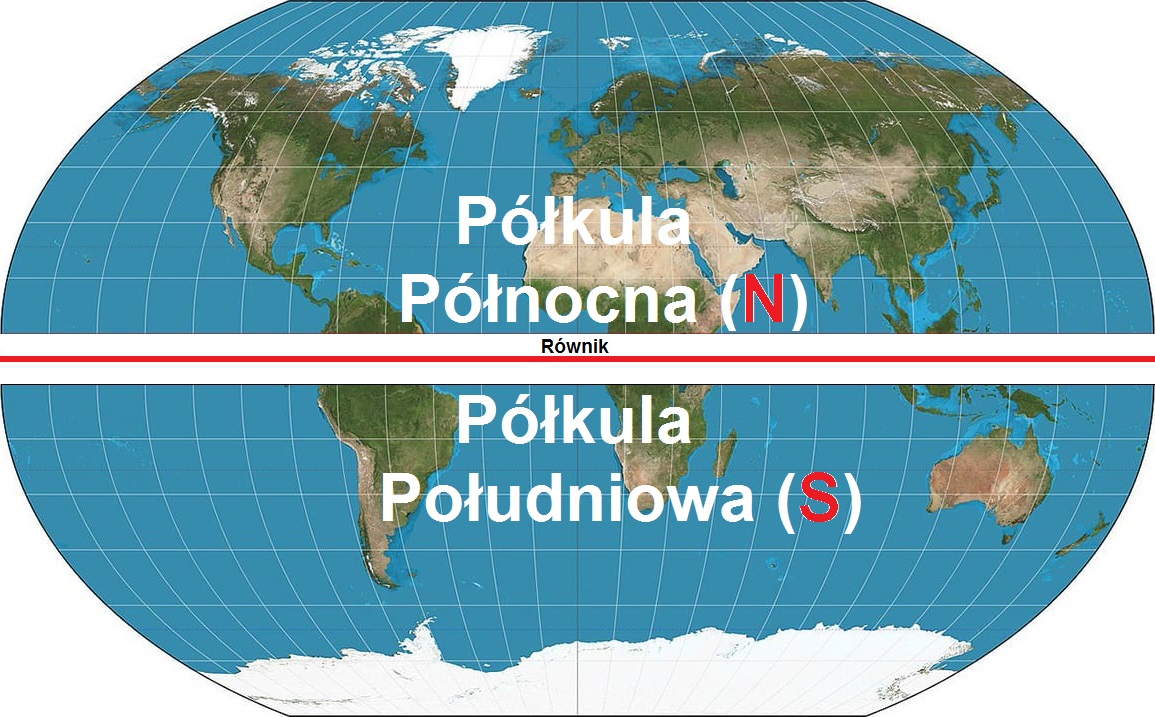
Podział Ziemi na półkulę północną (N) i południową (S) za pomocą równika
Źródło: Opracowanie własne na podstawie: https://www.onxmaps.com/hunt/blog/gps-global-positioning-complete-guide
Podział Ziemi którego dokonuje się za pomocą równika pozwala nam wytyczyć półkulę północną oraz półkulę południową. Półkula północna na mapach jak i na globusie to ta część Ziemi, która znajduje się “powyżej” linii równika. Półkula południowa jest z kolei “poniżej” linii równika. Półkule oznacza się dodatkowo literami: N – półkula północna oraz S – półkula południowa. Odnosi się to do anglojęzycznych nazw kierunków świata – N czyli North (północ) oraz S czyli South (południe).
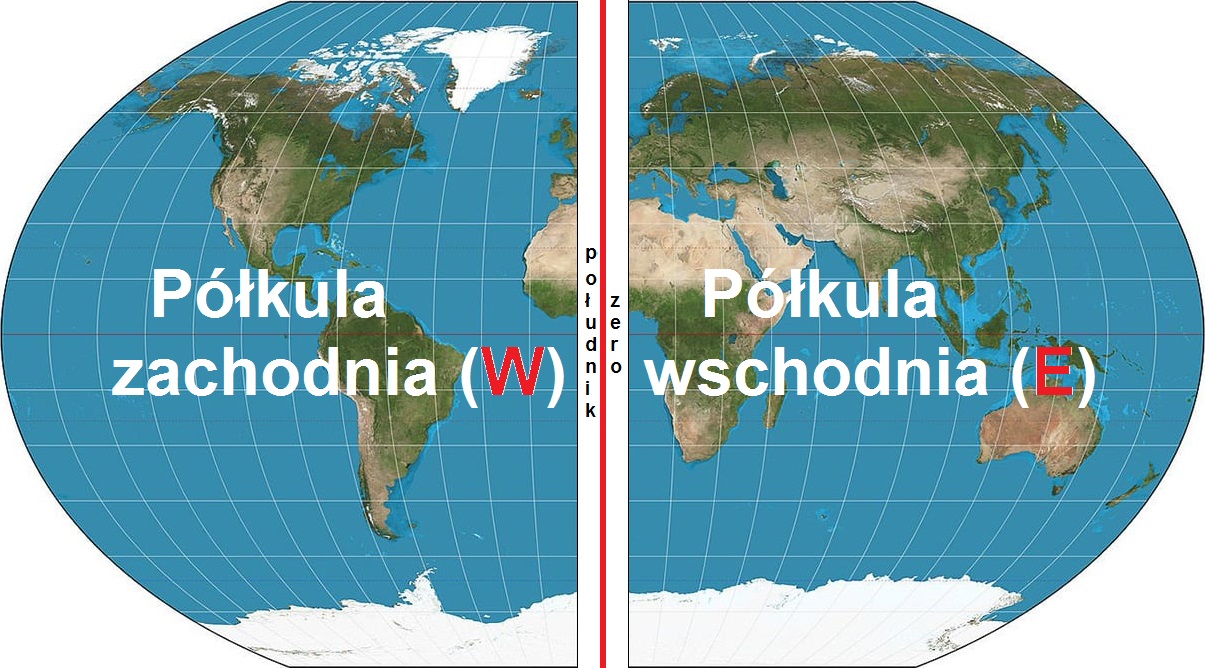
Podział Ziemi na półkulę zachodnią (W) i wschodnią (E) za pomocą południka zero
Źródło: Opracowanie własne na podstawie: https://www.onxmaps.com/hunt/blog/gps-global-positioning-complete-guide
Podział Ziemi którego dokonuje się za pomocą południka zero (początkowego) pozwala nam wytyczyć półkulę zachodnią oraz półkulę wschodnią. Półkula zachodnia na mapach jak i na globusie to ta część Ziemi która znajduje się “po lewej” od linii południka zero. Z kolei “po prawej” od niego znajduje się półkula wschodnia. Granicę podziału zamyka z drugiej strony południk 180° – przedłużenie południka zero po drugiej stronie planety.
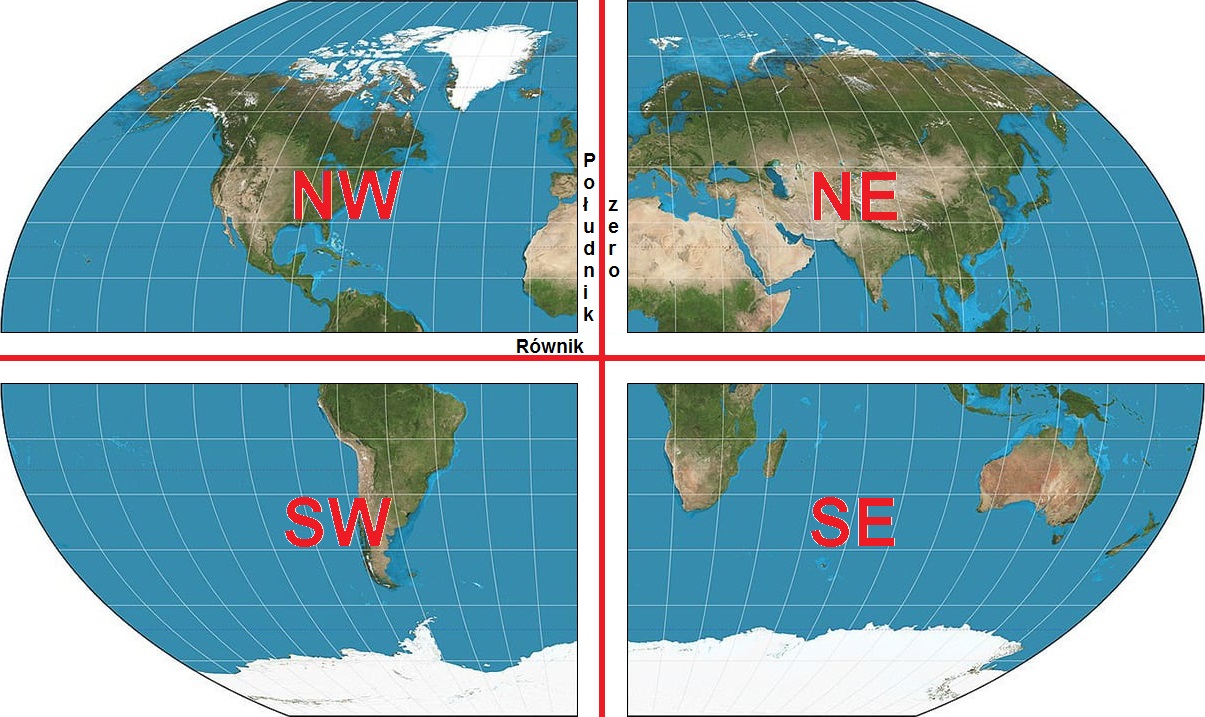
Podział Ziemi północ-południe i zachód-wschód jednocześnie – cztery ćwiartki Ziemi
Źródło: Opracowanie własne na podstawie: https://www.onxmaps.com/hunt/blog/gps-global-positioning-complete-guide
Za pomocą równika i południka zero można dokonać też podziału Ziemi jednocześnie – tworząc w ten sposób cztery ćwiartki planety i wyznaczając cztery główne części świata: północny-wschód (NE), południowy-wschód (SE), północny-zachód (NW) i połuniowy-zachód (SE). Umożliwia to wyznaczenie głównych kierunków Świata. Należy pamiętać, że podział północ-południe (N-S) ma pierwszeństwo przed podziałem zachód-wschód (W-E). Można także wyznaczać pomiędzy nimi kierunku pośrednie – tworząc w ten sposób kompas geograficzny zwany różą wiatrów.
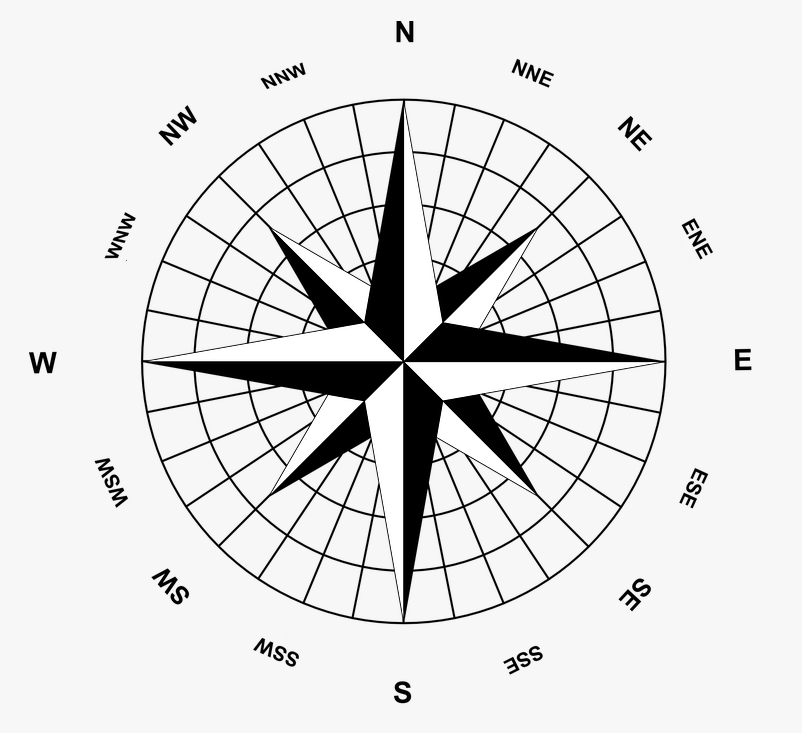
Uproszczony model róży wiatrów
Źródło: Jan Helebrant, https://www.pngitem.com/pimgs/m/347-3478879_geography-map-compass-rose-plot-travel-world-wind.png
3. Szerokość i długość geograficzna
Istnienie równoleżników i południków jest kluczowe dla wyznaczania dwóch parametrów położenia geograficznego punktów i obiektów, jakimi są: szerokość geograficzna oraz długość geograficzna. Podobnie jak w matematyce, parametry te umożliwiają matematyczne określenie “odległości” punktu od osi odniesienia. W matematyce osiami tymi są X oraz Y, a w geografii – równik oraz południk zero (0°) czyli południk początkowy.
Szerokość i długość geograficzna przedstawiona graficznie (kliknij aby powiększyć)
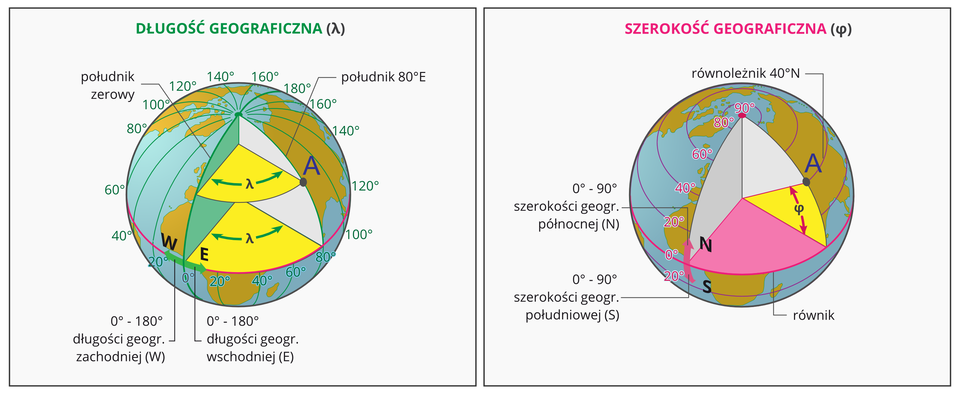
Źródło: https://static.epodreczniki.pl/portal/f/res-minimized/RzzCDAUMasqFL/11/960/fnHPcdVWlgebBkLGJRXZTBABNhujxppn.png
Szerokość i długość geograficzną wyrażamy w stopniach kątowych (°). Wyznacza się je jako kątową odległość po powierzchni Ziemi względem osi odniesienia – równika lub południa 0°. Odległości tę będą więc miały charakter łuku (nie linii prostej – ponieważ biegną po kulistej Ziemi).
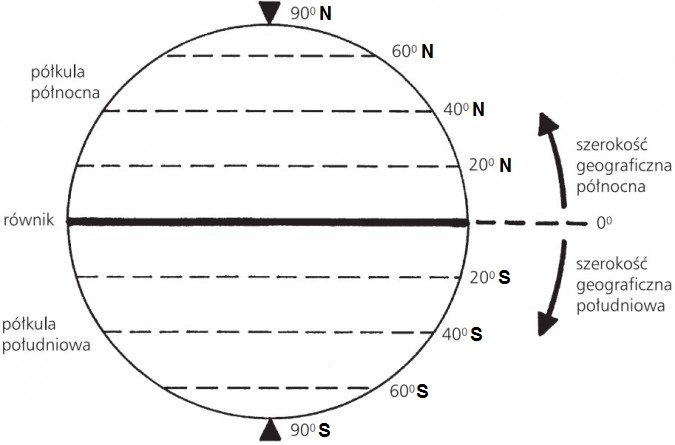
Pierwszym krokiem w geografii jest zawsze najpierw wyznaczenie szerokości geograficznej. Jest tą kątowa odległość punktu od równika, mierzona po powierzchni Ziemi. Ponieważ równik dzieli Ziemię na dwie połowy – północną i południową, szerokość geograficzna będzie miała charakter rosnącej – wraz z odległością od równika – wartości kątowej o kierunku północnym lub południowym.
Wyznaczanie szerokości geograficznej na schemacie globu
Źródło: https://opracowania.pl/opracowania/geografia/wspolrzedne-geograficzne,oid,628
Granicą szerokości geograficznej są bieguny – ostatnie z równoleżników. Względem nich z równika można więc wytyczyć maksymalnie kąt prosty. Z tego powodu szerokość geograficzna przyjmuje wartości od 0° (równik) do 90° szerokości geograficznej północnej (w skrócie: 90°N) lub 90° szerokości geograficznej południowej (w skrócie: 90°S).
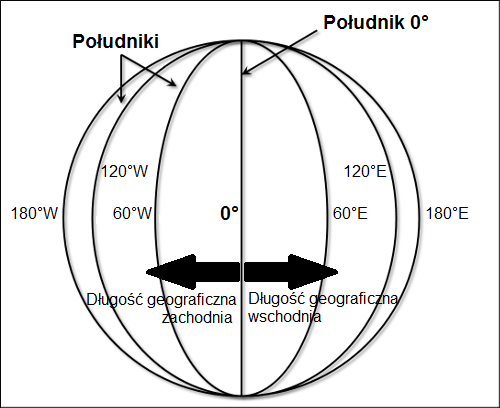
Analogicznie wyznacza się długość geograficzną, przy czym dla niej punktem odniesienia jest południk początkowy czyli południk 0°. Dzieli on Ziemię na półkule: zachodnią i wschodnią i takie też kierunki będzie przyjmować długość geograficzna.
Wyznaczanie szerokości geograficznej na schemacie globu
Źródło: Własna edycja na podstawie: https://gsp.humboldt.edu/olm/Lessons/GIS/01%20SphericalCoordinates/Latitude_and_Longitude.html
4. Współrzędne geograficzne na globusie i na mapie
Znając już podstawowe pojęcia i rozumiejąc mechanizmy wyznaczania, można przystąpić do odczytania z globusu i mapy współrzędnych geograficznych. Uprzedzając jednak to proste ćwiczenie, należy wspomnieć o zasadach prawidłowego zapisu współrzędnych. Zawsze najpierw odczytuje się i zapisuje wartość szerokości geograficznej, a potem długości geograficznej. Np. współrzędne Krakowa to: 50°N 20°E. Taki zapis oznacza, że Kraków leży na 50 stopniu szerokości geograficznej północnej i 20 stopniu długości geograficznej wschodniej. W trakcie nauki geografii konieczne stanie się odczytywanie punktów na różnych kontynentach, tak jak na poniższym przykładzie:
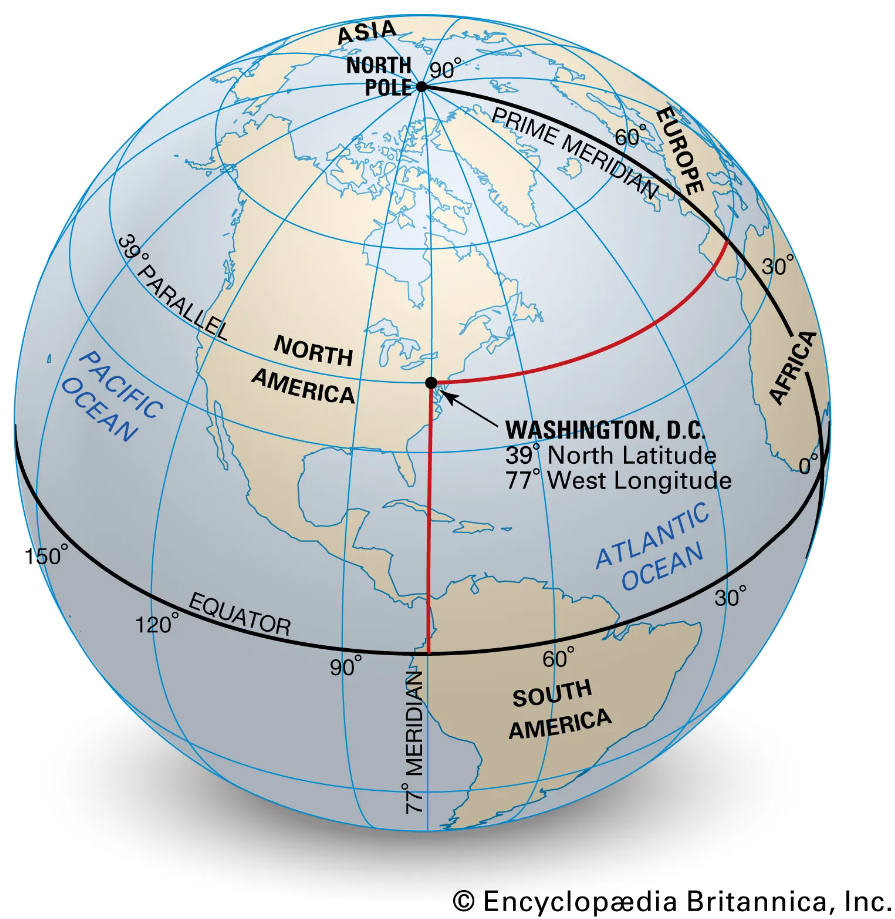
Wytyczenie współrzędnych miasta Waszyngton w USA, na modelu globusa Ziemskiego
Źródło: Encyclopædia Britannica, https://www.britannica.com/science/latitude#/media/1/331993/110281
*Equator – równik
*Prime meridian – południk początkowy (południk zero)
*Latitude – szerokość geograficzna
*Longitude – długość geograficzna
*Parallel – równoleżnik
*Meridian – południk
Odczytując współrzędne miasta Waszyngton, na globusie wyznaczono czerownymi liniami odniesienie odpowiednio do równika (equator) i południka 0° (prime meridian). Wskazano na mapie także dodatkowo równoleżnik (parallel) i południk (meridian), które odpowiadają wartościom Waszyngtonu. Z globusu możemy odczytać współrzędne: 39°N 77°W, a więc Waszyngton leży na 39 stopniu szerokości geograficznej północnej i 77 stopniu długości geograficznej.
Podobne ćwiczenie można wykonać na mapie. Tutaj jednak trzeba zdawać sobie sprawę, że ze względu na dużą szczegółowość obszaru często oprócz pełnych stopniu geograficznych, mogą pojawić się także minuty kątowe. W matematyce jednostki dzielą się zwykle na mniejsze części – podobnie jest w tym przypadku. 1 stopnień kątowy dzieli się na 60 minut kątowych. Zapisujemy to jako 1° = 60′. Wiedząc to, możemy określić bardziej precyzyjnie współrzędne szczegółowo oznaczonych na mapie obiektów. Zadania takie są znacznie trudniejsze i rozwiązują je osoby, które dobrze radzą sobie na poziomie pełnych stopni kątowych. Przykład przedstawiono poniżej:
Poniżej znajduje się mapa topograficzna – szczegółowa mapa danego terenu. Zaznaczono na niej punkt “A”, którego współrzędne należy odczytać z mapy.
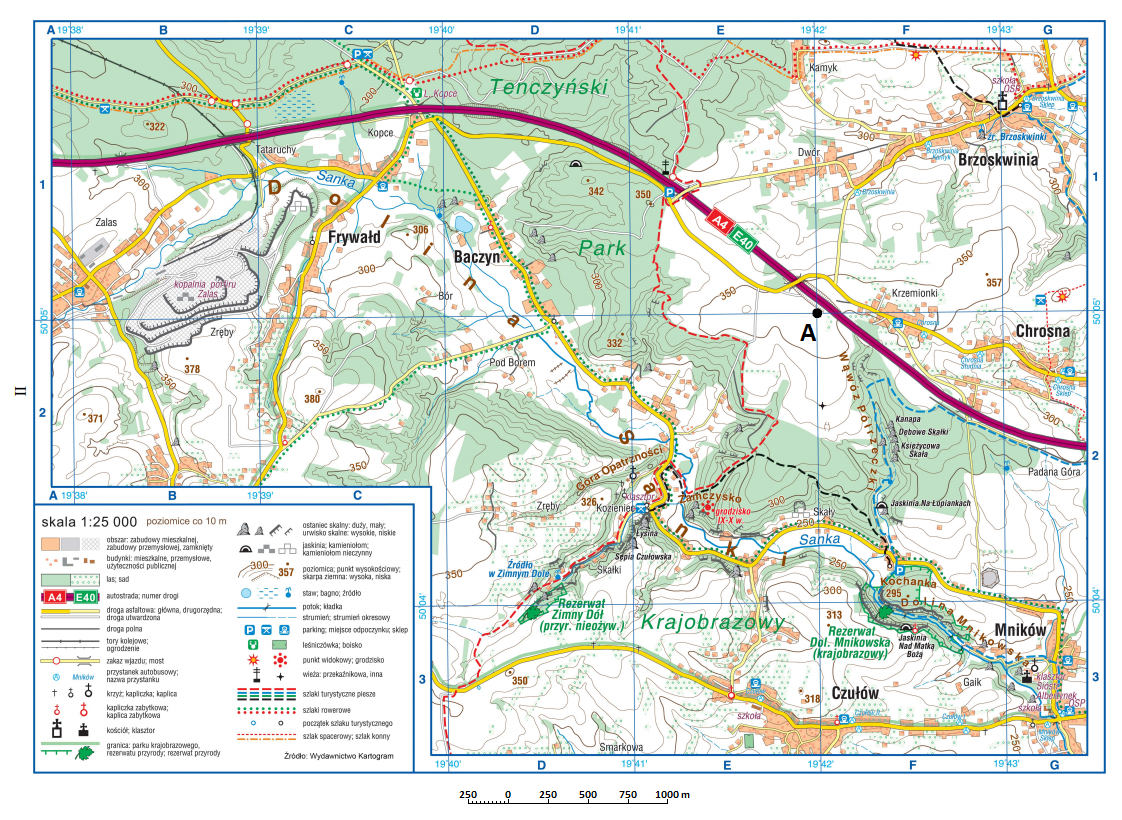
Zadanie łatwiej będzie rozwiązać, przyglądając się fragmentowi mapy blisko punktu “A”:
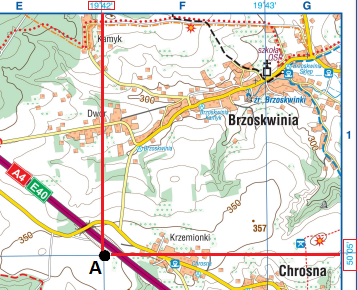
Punkt znajduje się idealnie na przecięciu równoleżnika i południka – wystarczy odczytać ich prawidłowe wartości, które znajdują się na marginesach mapy.
Zgodnie z zasadami określania położenia punktu, najpierw określamy szerokość geograficzną, a potem długość geograficzną. Po prawej stronie mapki widzimy na ramce wartość szerokości geograficznej – 50°05’N (bo mapa jest zorientowana ku północy). Z kolei nad obiektem A widzimy wartość długości geograficznej – 19°42’E (bo wartości rosną w kierunku wschodnim).
Prawidłowa odpowiedź: Współrzędne punktu A to: 50°05’N 19°42’E.
5. Zastosowanie odbiornika GPS w odczytywaniu współrzędnych
O ile określenie położenia punktu na mapie jest możliwe w dość łatwy i precyzyjny sposób, w geografii odwiecznym problemem było precyzyjne określenie położenie obiektów bez dostępu do map, albo obiektów na nich niezaznaczonych np. pozostających w ciągłym ruchu. Przełomem było stworzenie w latach 70-tych systemu GPS czyli Global Positioning System.
System oparty jest na pracy krążących wokół Ziemi satelitów nawigacyjnych. Dzięki emitowanemu sygnałowi radiowemu (zawierającemu informację o pozycji i dokładnym czasie), można obliczyć odległość satelity od naziemnego odbiornika. Jeżeli odbiornik znajdzie się w zasięgu minimum 4 satelitów, można określić jego położenie – szerokość geograficzną, długość geograficzną i wysokość nad poziomem morza. Im więcej satelitów obejmie swoim zasięgiem dany odbiornik, tym dokładniej ustalana jest jego pozycja. Aby każdy punkt na Ziemi mógł znaleźć się w zasięgu minimum 4 satelitów, potrzeba dokładnie 24 satelitów na orbicie – obecnie jest ich znacznie więcej.
Określanie dokładnego położenia geograficznego może być przydatne w czasie prowadzenia badań terenowych, albo zwiedzaniu. W tym celu można skorzystać np. z witryny internetowej google maps (maps.google.pl). Załóżmy, że prowadziliśmy badania w Warszawie pod Salą Kongresową Pałacu Kultury i Nauki – tuż przy przejściu dla pieszych wzdłuż ulicy Emilii Plater. Po zaznaczeniu miejsca w których staliśmy, Google podaje nam dokładne współrzędne punktu zapisane w postaci numerycznej. Można je potem przekształcić na współrzędne geograficzne znane nam z przykładów powyżej.
Nawet bez wychodzenia z domu, możemy określić położenie dowolnego punktu
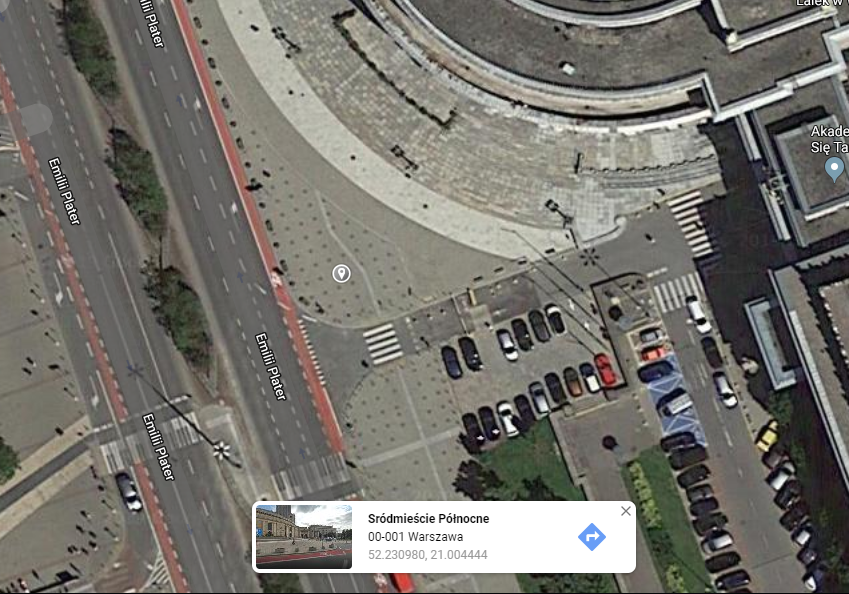
Źródło: https://www.google.pl/maps (widok satelity)
Podobne możliwości stwarzają nam także liczne aplikacje telefoniczne. Jedną z nich jest również google maps. Aby uzyskać własne położenie należy:
- Włączyć aplikację Google Maps.
- Uruchomić funkcję GPS w telefonie.
- Po naciśnięciu przycisku lokalizacji w prawym dolnym rogu ekranu, google wyświetli naszą aktualną pozycję na ekranie w postaci niebieskiej kropki.
Położenie autora w momencie tworzenia tego artykułu
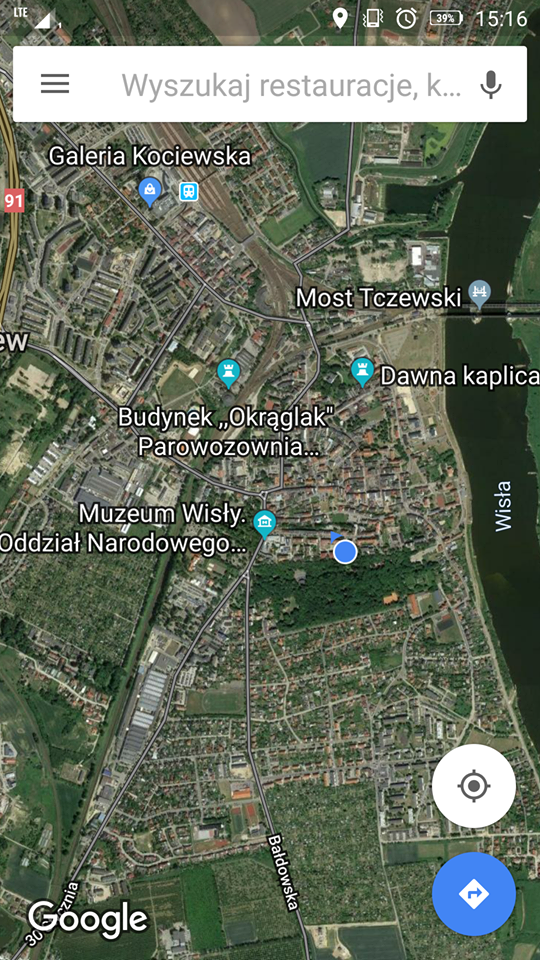
Źródło: Aplikacja google maps
Wielką zaletą GPS jest możliwość wykorzystania ich w turystyce albo w transporcie. Pozwalają nam określać nasze położenie, mierzyć odległości czy wytyczać trasy podróży, a także lokalizować w sąsiedztwie przydatne dla nas obiekty, np. restauracje, parkingi czy muzea.
Brak komentarzy