Umiejętność wyznaczania współrzędnych geograficznych należy do ważnych umiejętności często wykorzystywanych w geografii. Nie należy to jednak do zadań najprostszych – stąd konieczność ćwiczenia na wielu różnych przykładach – globusach, mapach czy siatkach przeznaczonych do ćwiczeń.
Spis tematów (kliknij, aby przejść do wyboru tematów)
Współrzędne w geografii
II Współrzędne geograficzne – ćwiczenia
1. Współrzędne geograficzne na uproszczonej siatce
Znając już zasady określania współrzędnych oparte o szerokość i długość geograficzną, warto przećwiczyć na praktycznych przykładach wyznaczanie współrzędnych. Przed przystąpieniem do bardziej ambitnych zadań opartych o globus czy mapę, warto sprawdzić się na uproszczonej siatce – układzie współrzędnych.
Zadanie 1 – na siatce poniżej określ położenie punktów A, B, C, D (tylko stopnie, bez minut)
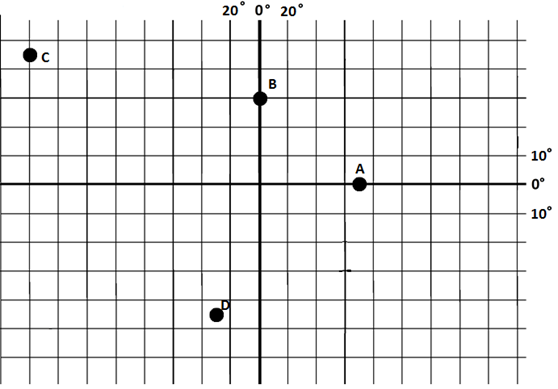
Źródło: Opracowanie własne.
Rozwiązanie zadania krok po kroku:
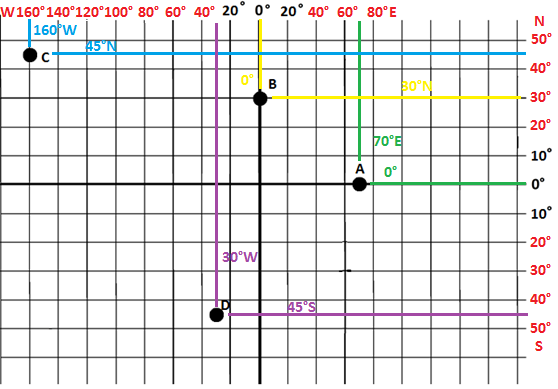
Źródło: Opracowanie własne
- Należy rozpocząć od określenia współrzędnych kolejnych równoleżników i południków. W tym zadaniu równoleżniki występują co 10°, a południki co 20°. Ponieważ liczba południków i równoleżników jest nieskończenie duża, można określić w takim zadaniu dowolne z nich.
- Poza samymi współrzędnymi należy także prawidłowo odczytać kierunki świata (N/S i W/E) – co ułatwiają umieszczone na rysunku równoleżnik 0° i południk 0°.
- Po ustaleniu współrzędnych siatki kartograficznej, należy dokonać prawidłowego odczytu poszczególnych punktów – najpierw odczytując szerokość geograficzną, a więc współrzędną z osi pionowej, a następnie długość geograficzną – współrzędną z osi poziomej.
- Jeżeli punkt leży dokładnie pomiędzy liniami siatki – należy przyjąć wartość środkową pomiędzy wartościami znanymi. Np. D leży dokładnie w połowie drogi między 40°S i 50°S – współrzędna wynosi więc 45°S, analogicznie druga współrzędna leży dokładnie pomiędzy 20°W i 40°W więc wynosi 30°W.
- Należy pamiętać o prawidłowym zapisie z uwzględnieniem kierunków geograficznych.
Prawidłowe odpowiedzi: A = 0° 70°E, B = 30°N 0°, C = 45°N 160°W, D = 45°S 30°W.
Zadanie 2 – na siatce poniżej określ położenie punktów A i B (stopnie i minuty)
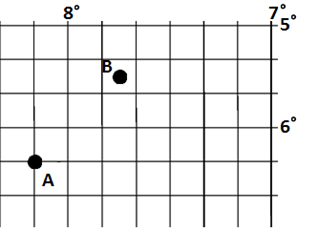
Źródło: Opracowanie własne.
Rozwiązanie zadania krok po kroku:
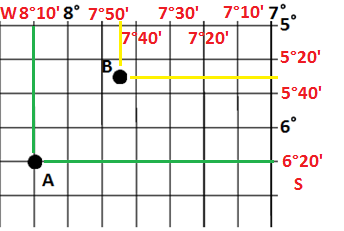
- Podobnie jak w zadaniu pierwszym – określamy współrzędne linii siatki. W tym zadaniu linie szerokości geograficznej przebiegają co 0°20′, a długości geograficznej co 0°10′. Wiemy to – na podstawie ilości linii pomiędzy pełnymi stopniami kątowymi.
- Ustalamy kierunki świata. Na grafice niestety nie mamy przecięcia południka 0° i równika, wobec tego musimy wymyślić, która część całej siatki kartograficznej została przedstawiona w zadaniu. Współrzędne szerokości geograficznej rosną „w dół”, a więc w kierunku południowym – pierwszą współrzędną będzie więc S. Z kolei współrzędne długości geograficznej rosną „w lewo”, a więc w kierunku zachodnim – drugą współrzędną będzie więc W.
- Ustalamy współrzędne punktów – pamiętając o zapisie kierunków świata.
- B leży dokładnie pomiędzy znanymi nam równoleżnikami i południkami. Podobnie jak w zadaniu 1 należy określić ich wartość – jako środkową pomiędzy znanymi wartościami.
Prawidłowe odpowiedzi: A = 6°20’S 8°10’W, B = 5°30’S 7°45’W.
2. Wyznaczanie współrzędnych geograficznych na globusie i różnych rodzajach map
Będąc już wyćwiczonym w wyznaczaniu współrzędnych na uproszczonych modelach – siatki – układu współrzędnych, można podjąć podobne próby na globusach i mapach. Warto pamiętać że układ współrzędnych na globusie nazywamy siatką geograficzną, z kolei jego odwzorowanie na płaszczyźnie mapy nazywa się siatką kartograficzną. Jednak w obu przypadkach, dobre globusy i mapy (za wyjątkiem map tematycznych) posiadają zawsze jakiś układ współrzędnych, który umożliwia odczytania położenia obiektów.
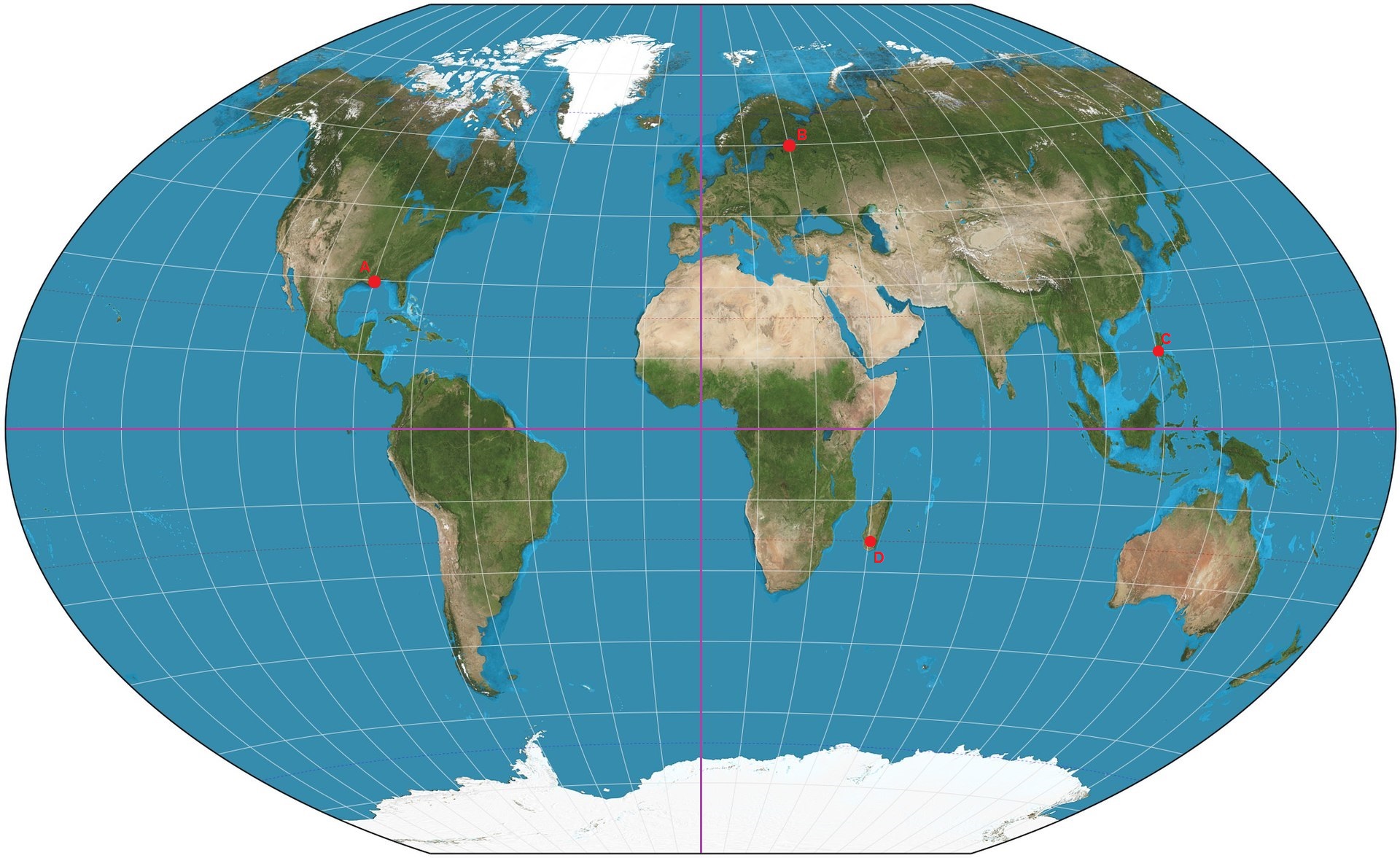
Zadanie 1 Wykorzystując mapę Świata określ współrzędne geograficzne punktów A, B, C i D
Mapa całej Ziemi z zaznaczonymi punktami (kliknij aby powiększyć)
Źródło: Strebe – domena publiczna; https://upload.wikimedia.org/wikipedia/commons/thumb/9/91/Winkel_triple_projection_SW.jpg/1920px-Winkel_triple_projection_SW.jpg
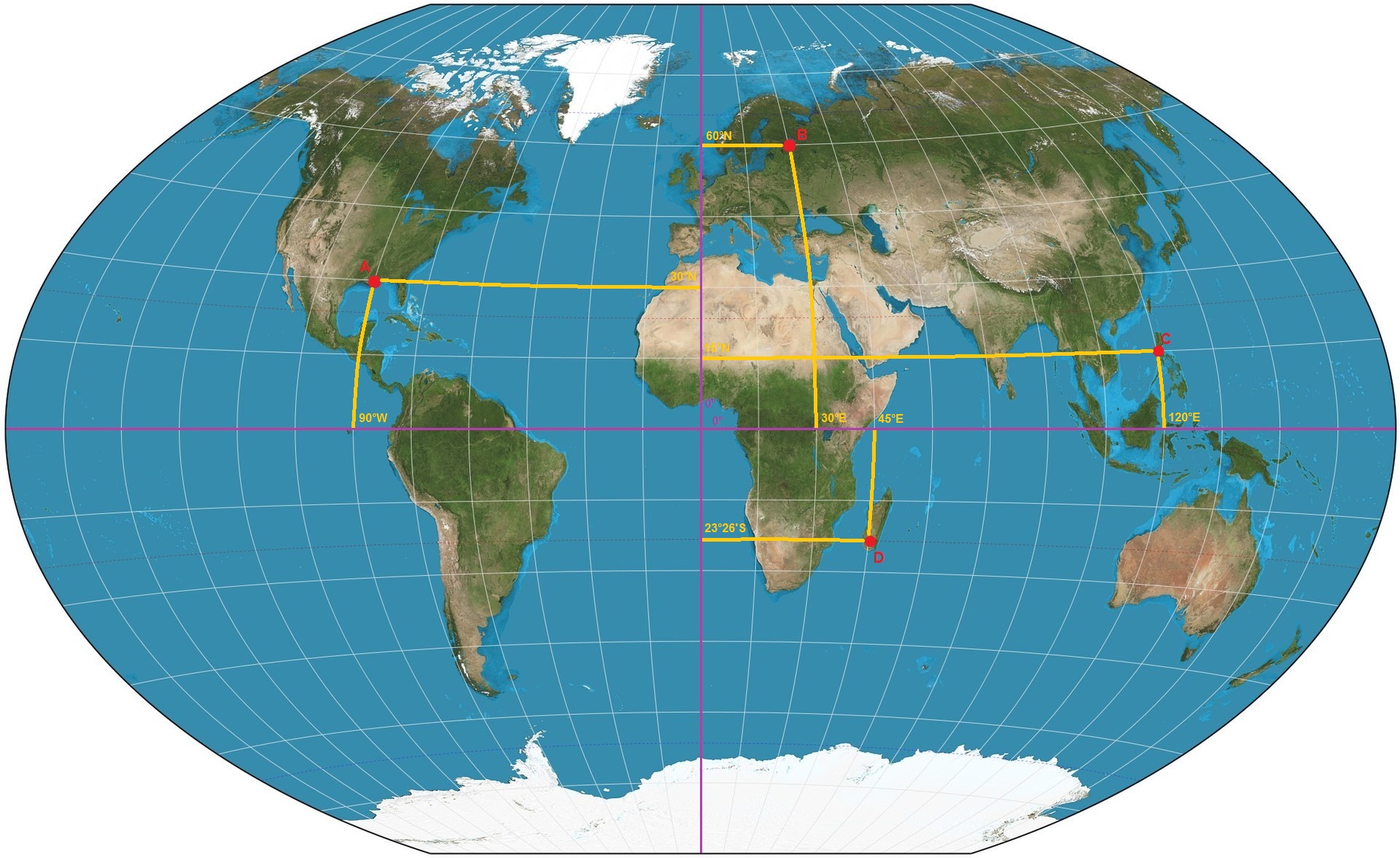
Rozwiązanie krok po kroku:
(kliknij na mapę aby powiększyć obraz z rozwiązaniem)
Źródło: Opracowanie własne na podstawie – Strebe – domena publiczna; https://upload.wikimedia.org/wikipedia/commons/thumb/9/91/Winkel_triple_projection_SW.jpg/1920px-Winkel_triple_projection_SW.jpg
- Na mapie do zadania zaznaczono liniami fioletowymi południk 0° oraz równik. Analizując układ siatki kartograficznej można zauważyć, że równoleżniki i południki wyznaczono co 15°. Wiedząc to, można określić precyzyjnie położenie każdego z punktów.
- Punkt A ma współrzędne 30°N 90°W. W tym miejscu znajduje się Nowy Orlean – największe miasto stanu Luizjana w USA.
- Punkt B to z kolei Petersburg – rosyjskie miasto i dawna stolica tego kraju o współrzędnych 60°N 30°E.
- Punkt C o współrzędnych 15°N 120°E nie wskazuje konkretnego istotnego obiektu, a jedynie miejsce na wyspie Luzon – największej w archipelagu Filipin.
- Punkt D znajduje się z kolei na Madagaskarze – czwartej największej wyspie Świata. Jego współrzędne wydają się być trudne do odczytania, ponieważ wymagają aby pamiętać, że linią przerywaną na mapach Świata zaznacza się zwrotniki i koła podbiegunowe. Punkt znajduje się na szerokości geograficznej Zwrotnika Koziorożca. Jego współrzędne to: 23°26’S 45°E.
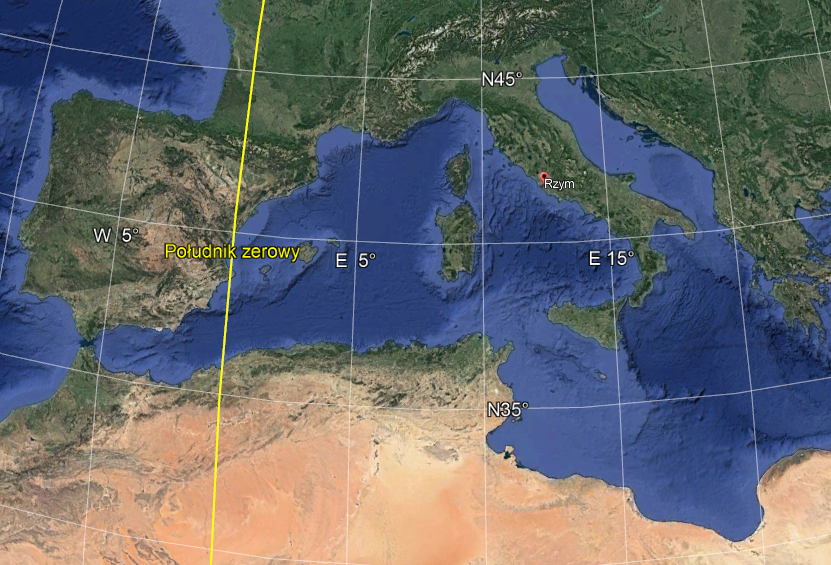
Zadanie 2. Wykorzystując fragment siatki geograficznej na modelu Ziemi w Google Earth określ współrzędne geograficzne Rzymu
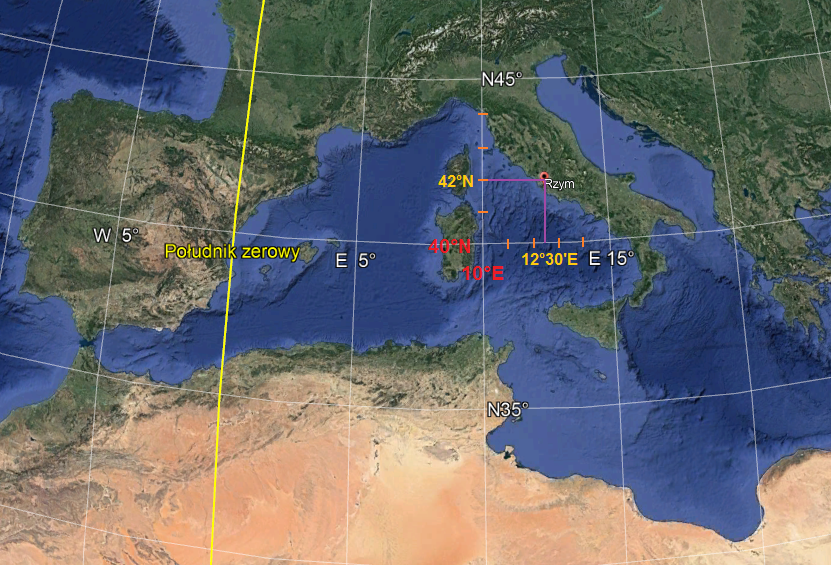
Siatka geograficzna na modelu Ziemi w Google Earth (kliknij, aby powiększyć)
Źródło: Google Earth
Rozwiązanie krok po kroku:
Źródło: Opracowanie własne na podstawie Google Earth.
- Wyznaczenie współrzędnych dla punktu, którego nie przecina na mapie (lub globusie – modelu Ziemi) żaden równoleżnik ani południk jest trudne, wymaga od nas aby samodzielnie wyznaczyć południki i równoleżniki pośrednie między tymi, które znajdują się już na siatce.
- Na powyższym przykładzie możemy zaobserwować, że oprócz Południka zero w sąsiedztwie Rzymu są: południk 5°E i 15°E oraz równoleżniki: 35°N i 45°N. Na tej podstawie możemy zauważyć, że oznaczenie siatek zmienia się o 5° tak w przypadku równoleżników jak i południków. Pozwala nam to wyznaczyć (oznaczone na mapie na czerwono) – równoleżnik 40°N i południk 10°E.
- Teraz, kiedy mamy już opisaną siatkę otaczającą Rzym z każdej strony, możemy zaobserwować, że miasto znajduje się w jej centrum. Konieczne jest więc wyznaczenie pośrednich równoleżników i południków – najlepiej proporcjonalnie, co 1°. Można to zrobić mierząc odległość między wybranymi fragmentami siatki i dzieląc ją na 5. W ten sposób udało nam się wyznaczyć równoleżniki między 40°N i 45°N oraz południki między 10°E i 15°E.
- Ciągnąć na schemacie prostopadłe linie do najbliższego równoleżnika i południka widzimy, że Rzym znajduje się niemal dokładnie na 42 równoleżniku północnym (42°N). W ten sposób wyznaczyliśmy szerokość geograficzną miasta. Nieco trudniejsza sytuacja dotyczy długości geograficznej. Przecięcie z południkiem nastąpiło niemal dokładnie w połowie, pomiędzy 12 i 13 południkiem wschodnim. W przybliżeniu wartość ta będzie więc wynosiła około 12 “i pół” południka. Ponieważ jednak w geografii każdy 1° dzieli się na 60′, to oznacza, że odległością pomiędzy 12° i 13° jest 12°30′. Współrzędna długości geograficznej Rzymu to więc (w przybliżeniu) 12°30’E.
Prawidłowa odpowiedź to: 42°00’N i 12°30’E.
- Jeżeli sprawdzimy precyzyjne położenie Rzymu w encyklopedii okaże się, że nasz wynik jest bardzo bliski prawdzie – a na tym poziomie możliwej precyzji – całkowicie prawidłowy. Ostatecznie współrzędne Rzymu to około 41°53’N i 12°29’E. Nasz błąd wynosił więc zaledwie kilka minut szerokości i jedną minutę długości geograficznej, co przy wielkości miasta Rzym jest różnicą nieistotną.
Zadanie 3 – Analizując mapę drogową określ współrzędne geograficzne południowych granic miasta Rzeszów z dokładnością do pełnych stopni
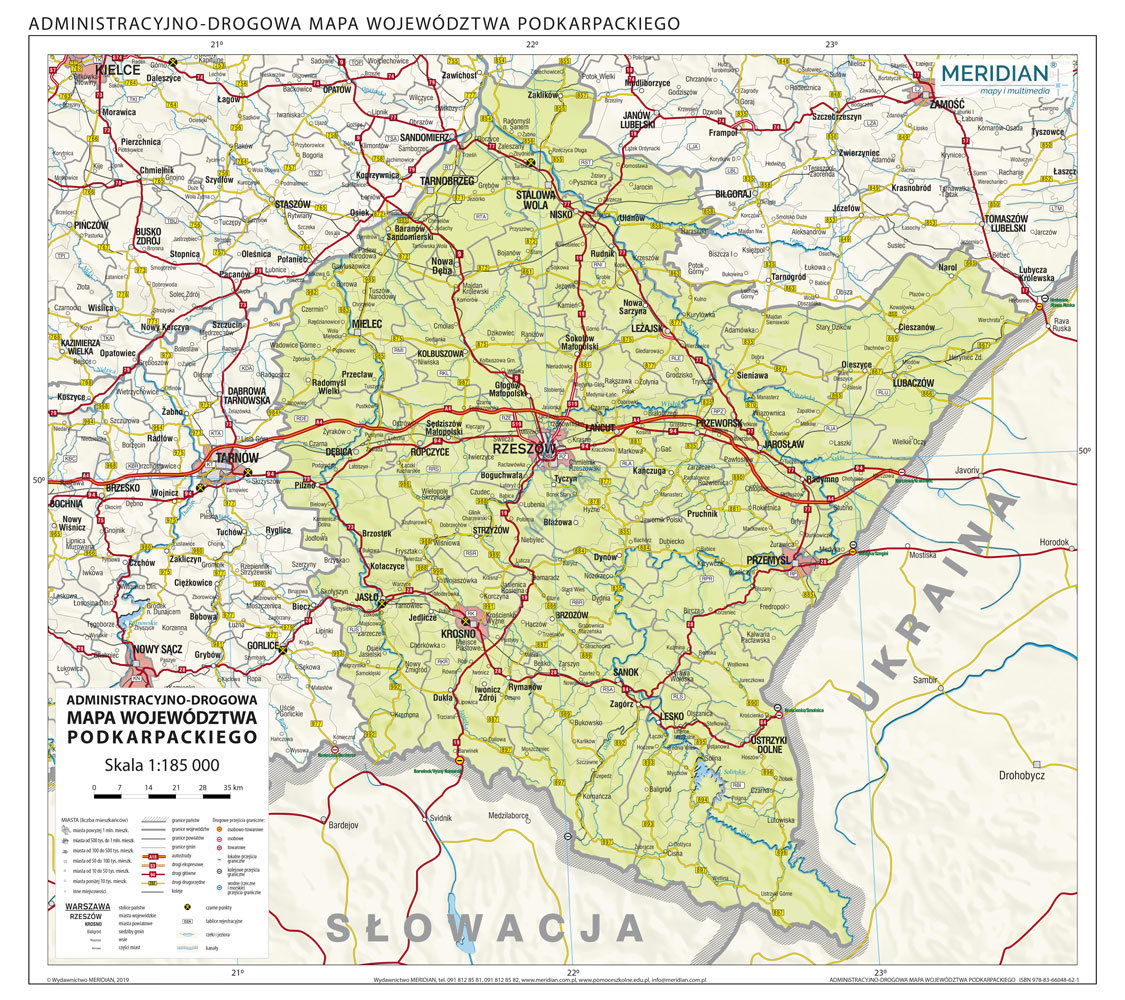
Mapa drogowa województwa podkarpackiego – kliknij aby powiększyć obraz
Źródło: https://www.pomoceszkolne.edu.pl/woj-podkarpackie-scienna-mapa-administracyjno-samochodowa.html
Rozwiązanie krok po kroku:
- Na powyższej mapie widoczne są współrzędne geograficzne, ale bez podanych kierunków Świata. Nie ma też na niej równika, ani południka 0°, które mogłyby być punktem odniesienia. Widzimy jednak, że południowe granice Rzeszowa przecinają linie o wartościach 50° i 22°.
- Określenie kierunków świata dla odczytanych wartości nie musi się wcale wiązać z posiadaniem szczegółowej wiedzy o Polsce ani posiadaniem innej mapy, na której można położenie Polski sprawdzić. W geografii obowiązuje bowiem prosta zasada, że brakujące fragmenty siatki kartograficznej (lub geograficznej) można sobie po prostu wyobrazić. W ten sposób można w pamięci dorysować sobie brakujące punkty odniesienia – równik i południk 0°.
- Ponieważ wartości szerokości geograficznej rosną “do góry” na mapie, a mapa jest zawsze zorientowana na północ, tzn. że im bardziej “do góry” tym bardziej na północ, możemy odgadnąć, że kolejny równoleżnik, który nie zmieścił się na mapie miałby wartość 51°, następny 52° itd. Patrząc więc w drugą stronę, tj “w dół mapy” brakujące równoleżniki miałyby wartości – 49°, potem 48° i tak dalej aż do osiągnięcia linii równika czyli 0°. Oznacza to, że obszar na mapie znajduje się na północ od równika, ponieważ wartości na mapie rosną “do góry”. Na tej podstawie możemy z całą pewnością stwierdzić, że szerokość geograficzna południowych granic Rzeszowa to 50°N.
- Analogicznie można postąpić w przypadku południków. Skoro na mapie widzimy kolejne rosnące wartości południków “w prawo” (21°, 22°, 23°), to znaczy, że poprzedzają je – po lewej stronie – południki: 20°, 19° i tak dalej aż do południka 0°. A więc skoro południk zero mamy “po lewej”, a wartości rosną “w prawo” – jesteśmy na wschód od południka 0° czyli na półkuli wschodniej. Dlatego z całą pewnością możemy stwierdzić, że długość geograficzna południowych granic Rzeszowa to 22°E.
Prawidłowa odpowiedź to: 50°N 22°E.
3. Odnajdywanie na mapie obiektów na podstawie współrzędnych
Nieco trudniejszym zadaniem jest prawidłowe odczytanie na mapie znanych nam współrzędnych, aby odszukać jakiś punkt. Wykonuje się to odwrotnej kolejności niż zadanie poprzednie – najpierw szuka się odpowiedniego równoleżnika i południka, a w miejscu ich przecięcia lokalizuje poszukiwany obiekt.
Zadanie 1 – Określ co znajduje się na poniższej mapie w miejscu o współrzędnych: 35°20’N i 25°08’E.
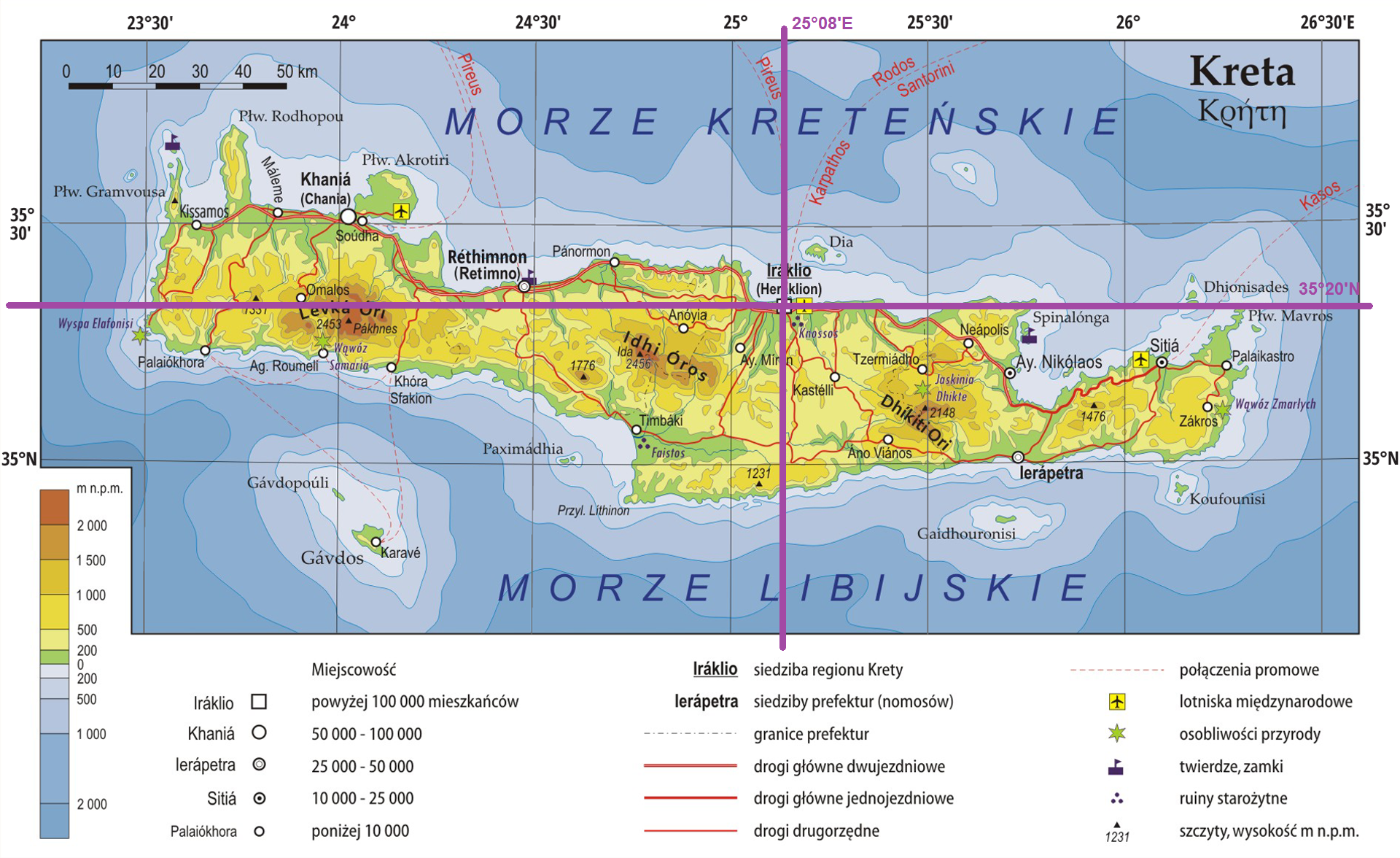
Mapa Krety
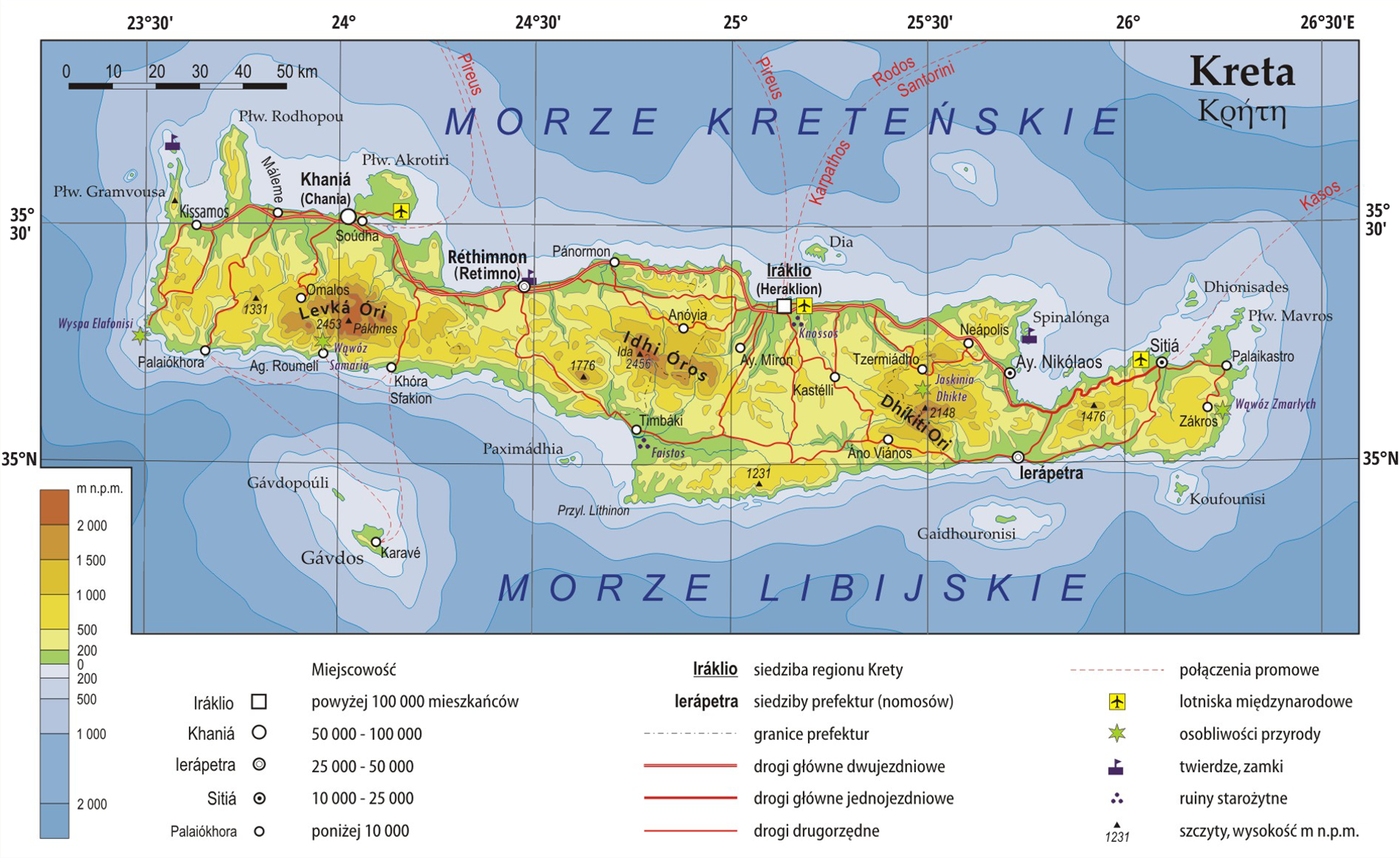
Źródło: https://static.epodreczniki.pl/portal/f/res-minimized/RgE6I9OqU9pkY/7/960/23sEhhH6qqSgvDS0uWMqjc9j4rCsHDGs.png
Rozwiązanie zadania krok po kroku:
Źródło: Własna edycja na podstawie: https://static.epodreczniki.pl/portal/f/res-minimized/RgE6I9OqU9pkY/7/960/23sEhhH6qqSgvDS0uWMqjc9j4rCsHDGs.png
- Posiadając współrzędne punktu, należy dokonać ich odnalezienia na mapie zgodnie z zasadą – najpierw szerokość, a później długość geograficzna.
- Współrzędne siatki zostały już podane. Kierunki świata również zostały wskazane, nie trzeba więc zgadywać – ale można analogicznie do zadania poprzedzającego – odczytać w którą stronę rosną wartości południków i równoleżników.
- Na mapie możemy zaznaczyć sobie nawet cały równoleżnik i południk o podanych współrzędnych, a poszukiwany punkt będzie w miejscu ich przecięcia – tak jak wykonano to na grafice powyżej.
Prawidłowa odpowiedź: Na podanych współrzędnych znajduje się miasto Iraklio (Heraklion)
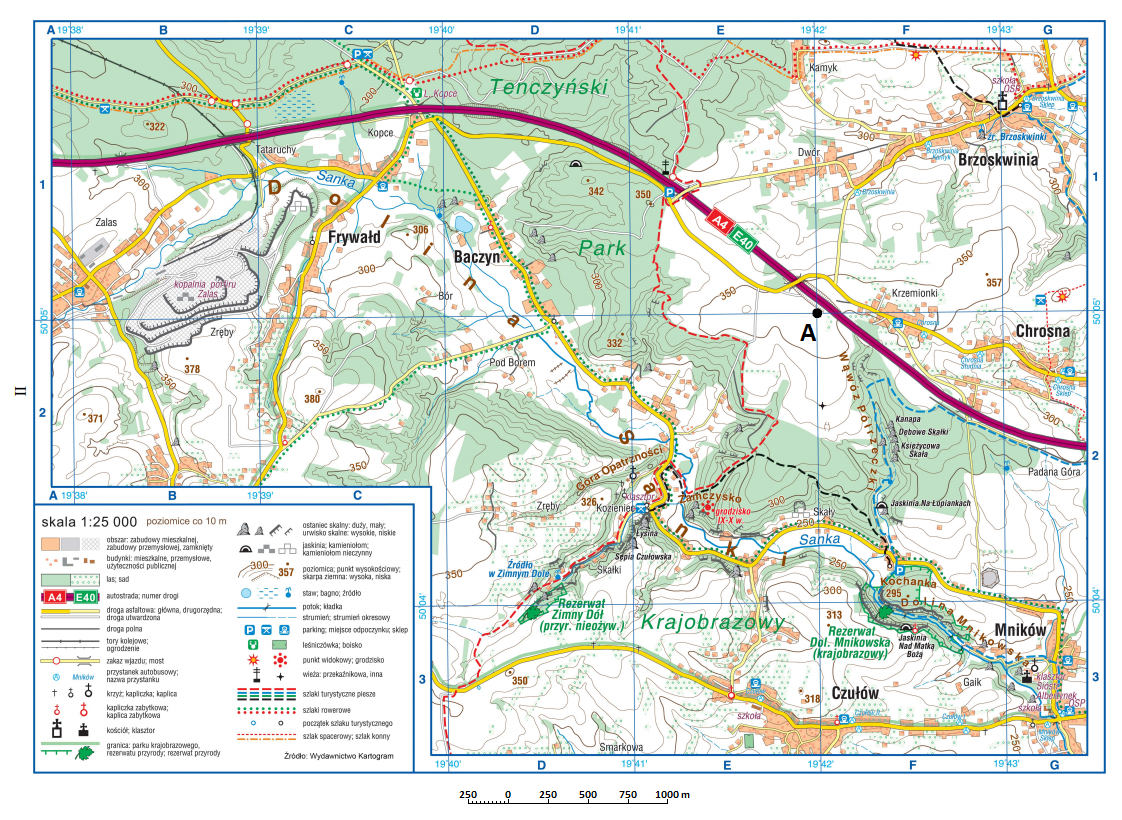
Zadanie 2 – Odszukaj obiekt przemysłowy, który na poniższej mapie znajduje się w sąsiedztwie miejsca o współrzędnych: 50°05’N 19°39’E.
Źródło: Matura z geografii 2018 – https://cke.gov.pl/images/_EGZAMIN_MATURALNY_OD_2015/Arkusze_egzaminacyjne/2018/formula_od_2015/geografia/Zalacznik.pdf
Rozwiązanie zadania krok po kroku:
- Na załączonej mapie topograficznej łatwo możemy zlokalizować przecięcie podanych wartości równoleżnika i południka – znajduje się ono w górnej-lewej części mapy, w dolnym-prawym rogu kwadratu B1.
- Z pomocą w zrozumieniu treści mapy przychodzi nam z kolei załączona legenda oraz opisy znajdujące się na samej mapie.
- Najbliższym obiektem przemysłowym w sąsiedztwie podanych współrzędnych jest Kopalnia porfiru Zalas.
Prawidłowa odpowiedź: Kopalnia porfiru Zalas.
4. Rozciągłość geograficzna
Pod pojęciem rozciągłości geograficznej rozumie się kątową odległość na mapie między jakimiś wybranymi obiektami. Możliwe jest np. policzenie rozciągłości kraju czy kontynentu. Do tego niezbędne są nam współrzędne tzw. skrajnych punktów czyli najdalej w danym kierunku wysuniętych fragmentów jakiegoś obszaru. Skrajne punkty bywają problematyczne, ponieważ w przypadku niektórych obiektów (np. kontynentów) może istnieć kilka skrajnych punktów w danym kierunku, co wynika np. z różnego zaliczania wysp, albo z rozumienia pod pojęciem skrajnego punktu jedynie obiektu na lądzie kontynentalnym, a nie np. na sąsiadującej z kontynentem wyspie.
Rozciągłość każdego obiektu można policzyć w dwóch osiach, tj. rozciągłość południkową i rozciągłość równoleżnikową. Pierwsza – rozciągłość południkowa – zgodnie z nazwą biegnie wzdłuż południka. A więc do jej obliczenia potrzebujemy wartości szerokości geograficznej dwóch wybranych punktów (skrajnego na północ i skrajnego na południe). Co ważne – ze względu na to, że wszystkie południki są tej samej długości, możliwe jest obliczenie wyniku nie tylko w stopniach kątowych, ale także w kilometrach. Zasada jest bardzo prosta – uzyskany wynik w stopniach należy pomnożyć razy 111,2 km. Wynika to z tego, że obwód Ziemi wzdłuż dwóch dowolnych południków po obu stronach planety wyniesie nieco ponad 40 000 km. Po podzieleniu tej wartości przez 360° (wartość kątowa okręgu) obliczymy, że – w zaokrągleniu – 1° = 111,2 km.
Druga z rozciągłości – rozciągłość równoleżnikowa – jak nazwa wskazuje, obliczana jest wzdłuż równoleżnika. Oznacza to, że do jej wyliczenia niezbędne są nam wartości długości geograficznej dwóch wybranych punktów (skrajnego na zachód i skrajnego na wschód). Niestety nie jest możliwe przeliczenie tej wartości na kilometry, ponieważ każdy równoleżnik jest innej długości i bez specjalistycznych tablic geograficznych nie można wyliczyć wartości w kilometrach dla 1° kątowego. Wynik pozostanie więc w stopniach kątowych.
Problem rozciągłości geograficznej może się wiązać z pewnymi kłopotami obliczeniowymi. Zaczniemy więc od najłatwiejszego przykładu – rozciągłości południkowej Afryki.
Przypadek pierwszy – najłatwiejszy
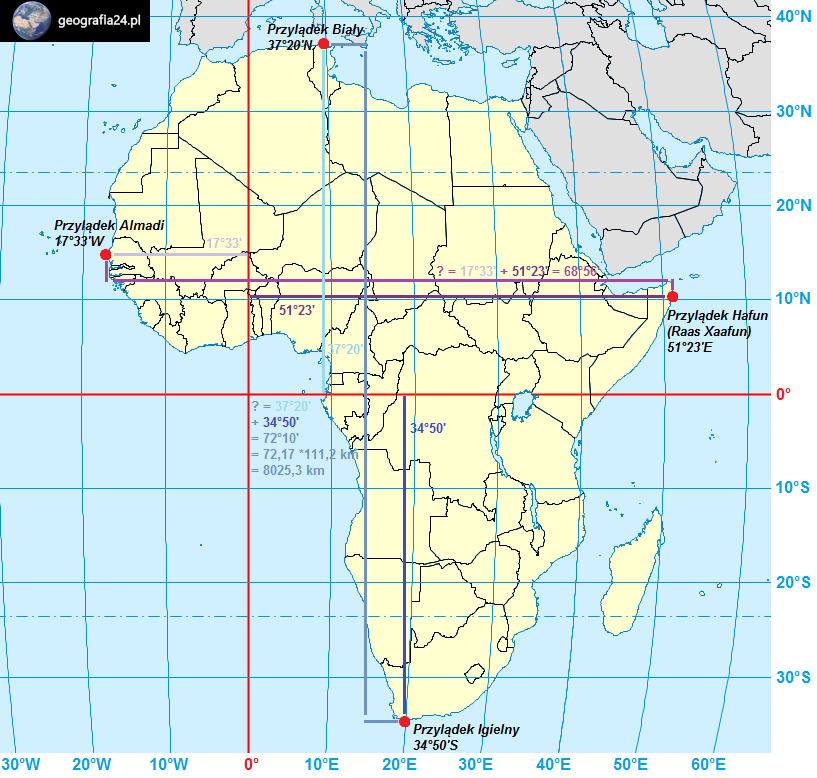
Za najłatwiejszy przypadek obliczania rozciągłości geograficznej uchodzi Afryka. Jest to spowodowane tym, że każdy z jej (lądowych) skrajnych punktów znajduje się na innej półkuli. Z rysunku (poniżej) wynika więc wprost, że aby uzyskać odległość między punktami, wartości ich skrajnej współrzędnej wystarczy dodać. Na rysunku oznaczono dodatkowo odległości kątowe od południka 0° i równika, aby ułatwić zrozumienie działania matematycznego.
Skrajne punkty Afryki i rozciągłość południkowa oraz równoleżnikowa
Źródło: Opracowanie własne.
Skrajnymi punktami Afryki są:
- Na północ – Przylądek Biały (37°20’N)
- Na południe – Przylądek Igielny (34°50’S)
- Na zachód – Przylądek Almadi (17°33’W)
- Na wschód – Przylądek Hafun (nowa nazwa – Raas Xaafuun) (51°23’E)
Po dodaniu wartości skrajnych punktów wzdłuż południków uzyskujemy rezultat 72°10′. Wartość tą możemy pomnożyć – tak jak to omówiono wcześniej – przez 111,2 km. Okaże się, że Afryka ma rozciągłość południkową ponad 8 000 km!. Z kolei w przypadku rozciągłości równoleżnikowej – po dodaniu wartości punktów uzyskamy wynik 68°56′.
Przypadek drugi – trudniejszy
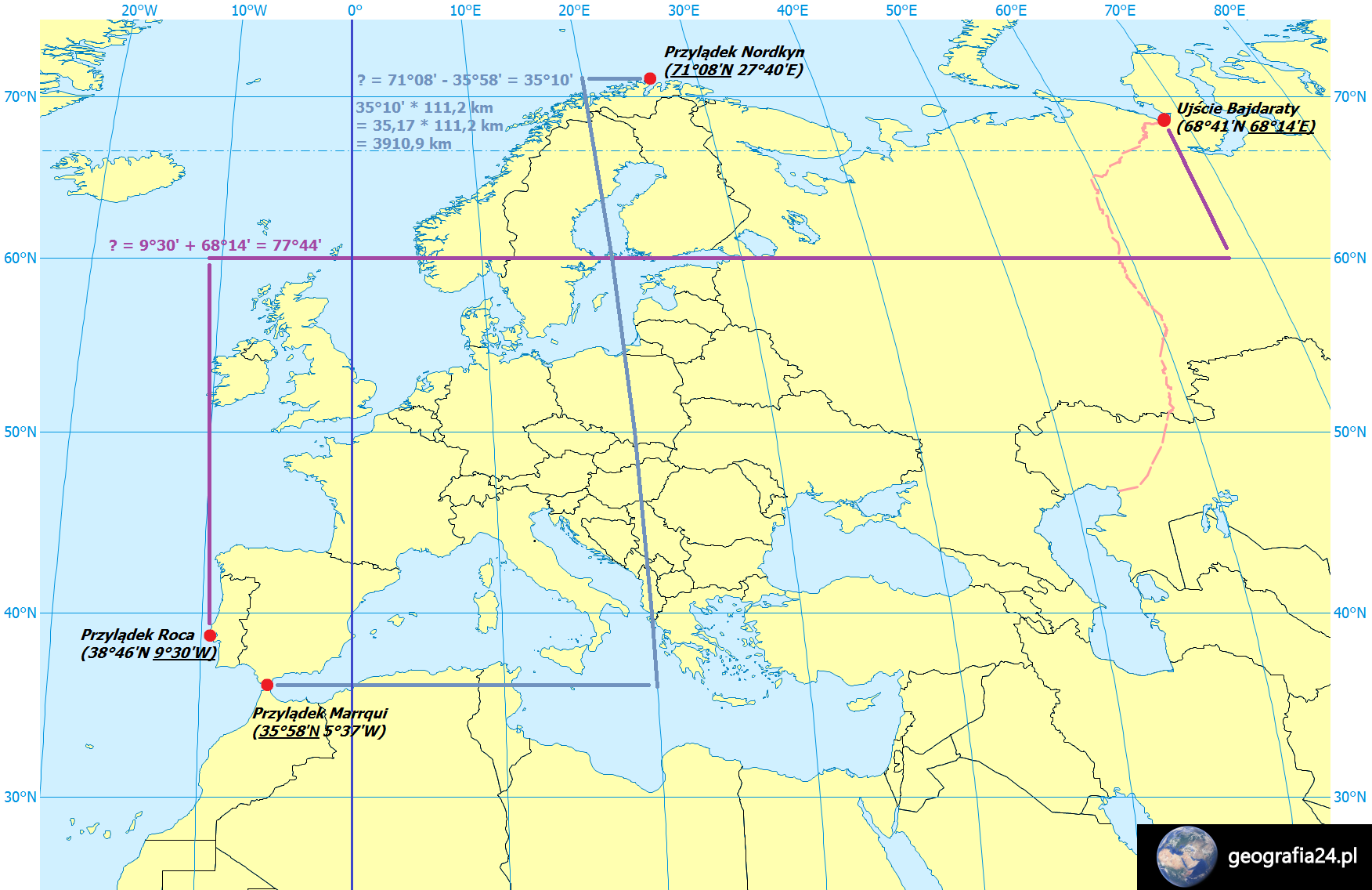
Nieco trudniejsze będzie obliczenie obu rozciągłości geograficznych wtedy, gdy kontynent znajduje się na tylko jednej z dwóch półkul – takim kontynentem jest np. Europa. Choć przez jej obszar przebiega południk 0° więc w przypadku długości geograficznej sytuacja obliczeniowa jest podobna jak w przypadku Afryki, to oba skrajne punkty szerokości geograficznej znajdują się na tej samej półkuli – północnej. W konsekwencji – najbardziej wysunięty na południe punkt kontynentu będzie miał współrzędną N ponieważ znajduje się wciąż na półkuli północnej – co dla wielu może być mylące.
Skrajne punkty Europy i rozciągłość południkowa oraz równoleżnikowa
Źródło: Opracowanie własne.
Skrajnymi punktami Europy są (w nawiasie skrajna współrzędna):
- Na północ: Przylądek Nordkyn (71°08’N)
- Na południe: Przylądek Marroqui (35°58’N)
- Na zachód: Przylądek Roca (9°30’W)
- Na wschód: Ujście rzeki Bajdaraty (68°14’E)
W tym przypadku rozciągłość południkową obliczamy poprzez odjęcie wartości skrajnych współrzędnych, ponieważ oba punkty leżą na półkuli północnej. Dzieję się tak, ponieważ szukaną wartością kątową jest różnica odległości między znanymi punktami. I tak: wiedząc, że Przylądek Marroqui jest 35°58’N od równika, a przylądek Nordkyn 71°08’N od równika, zastanawiamy się ile jest stopni pomiędzy Nordkyn i Marroqui?
W przypadku rozciągłości równoleżnikowej – należy je dodać (tak jak w przypadku Afryki), ponieważ punkty leżą na dwóch różnych półkulach. W rezultacie uzyskujemy informację, że rozciągłość południkowa Europy to 35°10′ (czyli ponad 3900 kilometrów), a równoleżnikowa: 77°44′.
Przypadek trzeci – najtrudniejszy
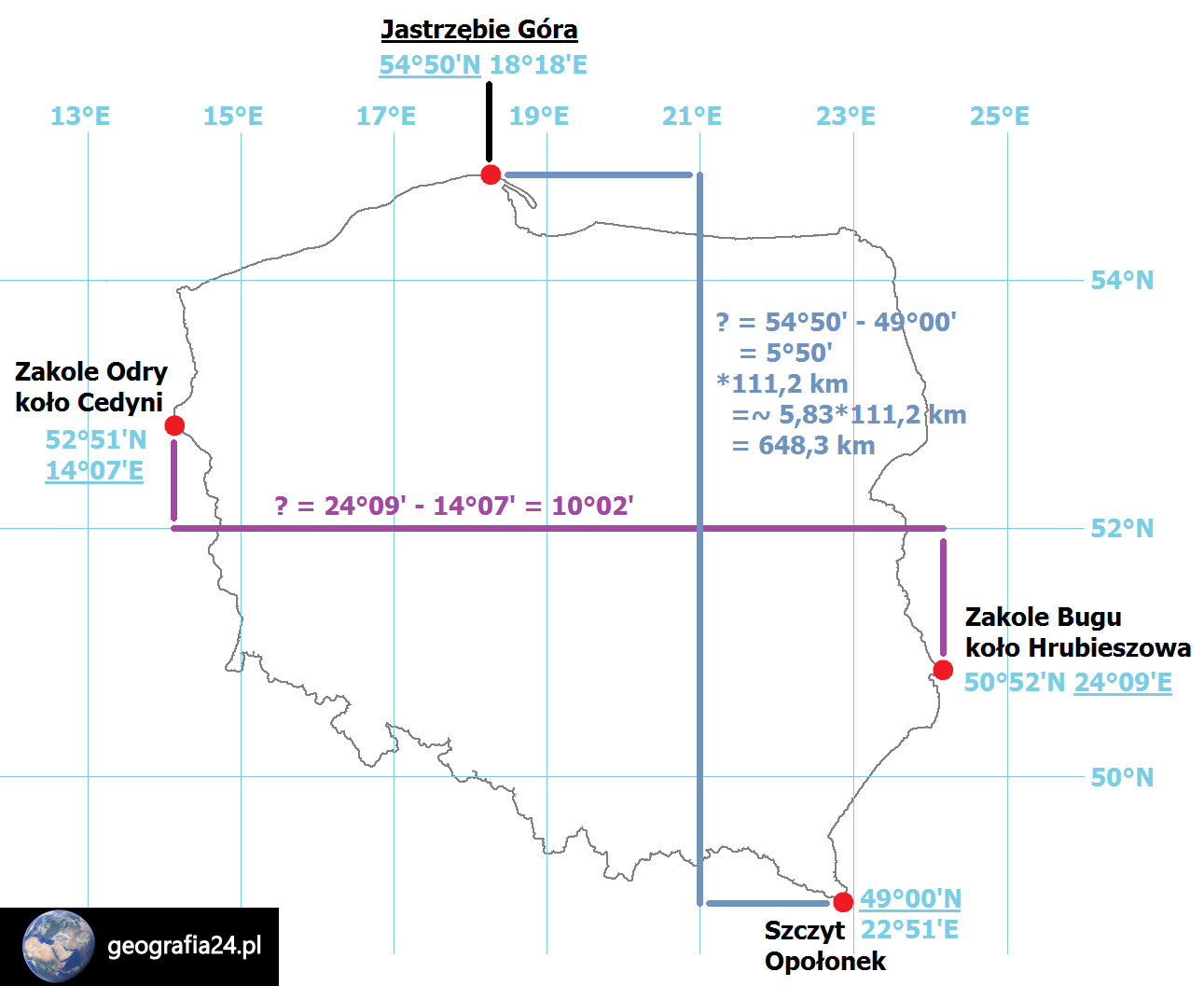
krajne punkty Polski i rozciągłość południkowa oraz równoleżnikowa
Źródło: Opracowanie własne.
Skrajnymi punktami Polski są (w nawiasie skrajna współrzędna):
- Na północ: Jastrzębia Góra (54°50’N)
- Na południe: Szczyt Opołonek (49°00’N)
- Na zachód: Zakole Odry koło Cedyni (14°07’E)
- Na wschód: Zakole Bugu koło Hrubieszowa (24°09’E)
W przypadku Polski mamy do czynienia z sytuacją, gdy ani równik, ani południk 0° nie znajdują się na jej terytorium. Polska znajduje się w całości na półkuli północnej i wschodniej. W związku z tym – analogicznie jak w przypadku rozciągłości równoleżnikowej Europy, przy obliczaniu obu rozciągłości wartości współrzędnych należy odjąć, ponieważ znajdują się one na tych samych półkulach. W rezultacie uzyskujemy informację, że rozciągłość południkowa Polski to 5°50′ (czyli niecałe 650 kilometrów bo 5°50′ = 5,83*111,2km =~ 648,3 km), a równoleżnikowa: 10°02′.
Brak komentarzy